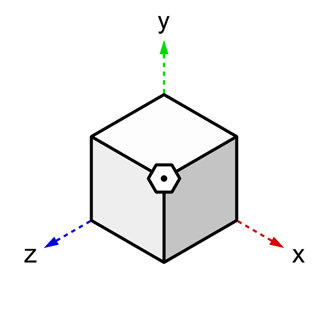
「4次元目の軸の発見用の図」などを使って、4次元目の軸を発見し、ψ3〜ψ4が明確の見えるようになってくると、空間がある形に歪んでくるイメージが出てくるようになります。

　まず、「3次元双曲面」というものがあります。
　これは、以下のような形の図形にあたります。「3次元双曲面」は、4次元空間上に存在するものにあたり、描画は難しいですが、この形は、4次元空間からの形が、3次元空間に擬似的に落とし込まれているような形になり、3次元空間上の「二葉双曲面」の形になります。（二葉双曲面では、二つの曲面が対になって形作られていますが、ここでは一方だけ見ていきます。）

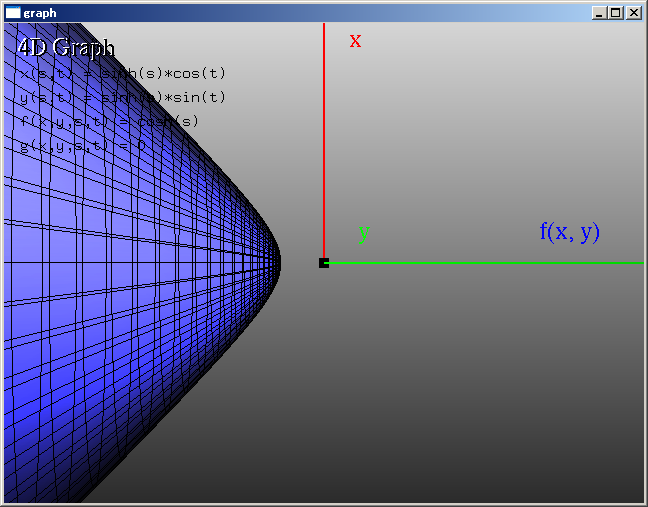
※この図は、「4d_graph」というフリーソフトを使って作成しました。（クリックで色々な角度から見る）

　3次元双曲面は、4次元目の軸を「w」とすると、以下のような方程式で表されます。　
　

　これは、3次元空間上では、「二葉双曲面」の形にあたるわけですが、「二葉双曲面」の方程式は、以下の式になります。
　

　それに対し、「3次元球面」というものがあります。これは、単純に、形としては「球」で表されるもので、「4次元空間を扱うにおいて出てくる球の形」といった所です。これも、4次元空間からの形が、3次元空間に落とし込まれるように形作られます。

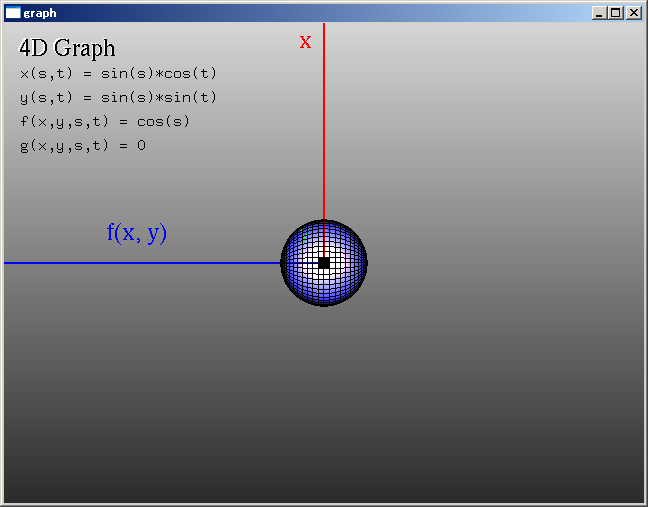
　方程式は、以下の式になります。
　

　これは、3次元空間上では完全に球の形になるので、以下の式で表されます。
　

　「球」と「二葉双曲面」は、2次元平面における「円」と「双曲線」のような関係にあり、ここに対化的な関係があります。

　さて、ここで、例の「4次元目の軸の発見図」で、4次元目の軸を発見している時を思い浮かべて欲しいです。これが出来ていて、ψ3もψ4も見えている時の空間の形は、「3次元球面」と「3次元双曲面」で表すと、以下のような構図の形に、歪んで見えるようになります。

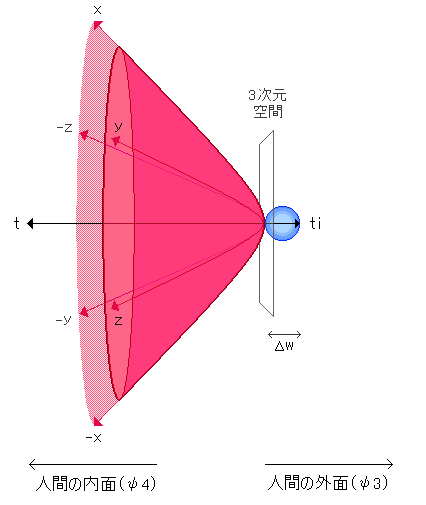
　この形は、より『ψ3』と『ψ4』の本性に近い形にあたります。

　まず、右側の青い球は、「虚数の直径を持つ微小球」にあたり、これが『人間の外面』から見た「モノ」にあたります。
　「Δｗ」というのは、ここでは、「無限小の大きさの4次元軸上の長さ」という意味になります。
　ψ3とψ4を知覚した状態であると、「モノ」は、ほとんど「点」として見えるようになります。『ψ3』もとい、『人間の外面』からモノを見ると、それは無限遠点先の位置からモノを見ることになるので、ありとあらゆるモノは、長さ「1/∞」のようなミクロ状態になり、普段感じている「距離」や「長さ」は、ほとんど機能しない状態になります。
　この「ψ3からみたモノ」は、無限小の大きさの球体へと、モノが縮め込まれてるイメージになります。
　また、『奥行き』も同様に、ほぼ無限小の長さに縮め込まれています。「見る」ではなく「観る」の状態のときは、『奥行き』に長さというのは、ほとんど存在しなくなります。これが、ヌーソロジー的な「世界はフラット（平面）である。」ということの真意です。
　この時の、真ん中の白い板は、「3次元空間」にあたります。ヌーソロジー的には、世界は、実はフラットな状態に畳み込まれていて、フラットな3次元空間と、「自分が作っている3次元空間のイメージ」、それから、「微小球に畳み込まれたモノ」によって、世界を見ています。

　それから、この領域において、時間は「ｔｉ」で表されていますが、ここでは、「通常の時間」というのは存在しません。ここに存在する時間は、哲学者ベルクソンの言葉を用いると、「持続的な時間」にあたります。

　ここで、「虚数の直径を持つ微小球」が上手くイメージできるようになると、『人間の外面』への参入がし易くなり、また、『最小精神』というものも芽生えてくるようになります。
　『最小精神』とは、ヌーソロジー用語であり、「『顕在化』における始めの位置」とされ、「主体の赤ちゃん」とも説明されるものです。
　この『最小精神』が発見できるようになると、ヌーソロジー的にも、精神的にも、心強いものが芽生えてくるようになります。

　一方で、左側の「3次元双曲面」は、「ψ3側から見た通常空間」にあたり、『人間の内面』側にあるものになります。また、これが『人間の内面』にあるとされる、「3次元空間のイメージ」を作っているものにも該当します。
　つまり、ψ3〜ψ4を知覚した状態における、「ψ4の作る3次元空間の想像（イメージ）」になります。これは、無限大へと世界が広がってくイメージになります。
　また、ここに存在する時間は、「ｔ」で表されていますが、これは、「通常の時間」です。『人間の内面』側には、ごく普通の時間が存在するということです。これは、物理学的な言葉を用いると、「近質的な時間」にあたります。

　それから、「3次元双曲面」について一つ補足をすると、「3次元双曲面」においては、「x,y,z」の軸はそれぞれ、以下のような方向にあります。　

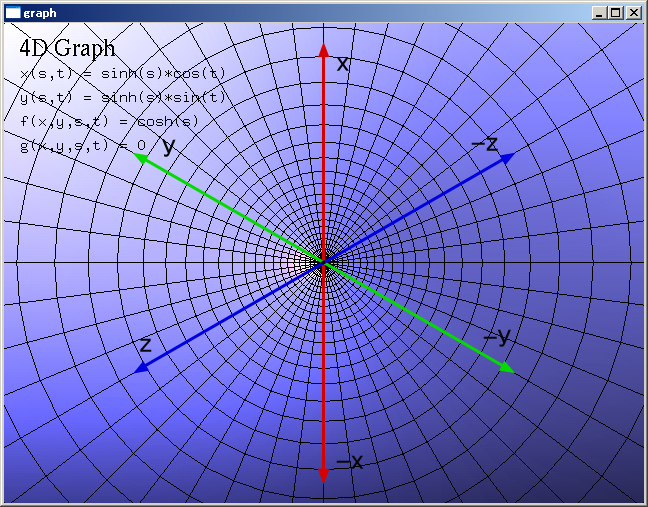
（3次元双曲面を正面裏側から見た図）

　「3次元双曲面」にあるとされる「3次元空間のイメージ」も、このような軸が向いている形で、畳み込まれているわけです。　
　

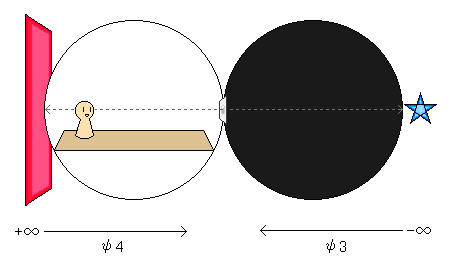
　そして、「3次元球面」と「3次元双曲面」で表されるこの構図は、『主体』と『客体』の位置にも対応しています。　
　「無限小へと縮んでいる3次元球面」は「前」、「無限大へと広がっている3次元双曲面」は「後ろ」方向に位置します。

　こうした空間の歪曲の仕方が見えるようになると、より一層、知覚が定着してくるようになります。