これから、「4次元」や、その次の「5次元」という存在について述べていきます。

　まず、オコツトは「4次元対称性」や「5次元対称性」というものについて言っていました。
　これらの対称性については、コウセンさんは、最近、言及しなくなってきましたが、ここでこれについて言及してみます。

　「4次元対称性」を理解するあたって、先に「4次元球面」というものについて知っておく必要があるので、それについて説明します。 　
　まず、4次元を見ている状態を意識してみます。

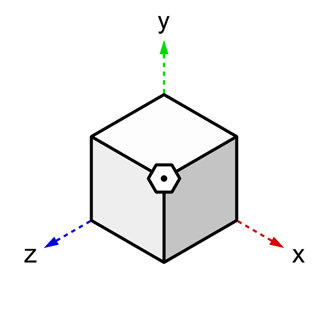
　先程も出てきた、「4次元目の軸を発見するための図」です。
　この図に描かれている立方体を、「平面」として捉えるように見ます。

　そして、それを回転させます。

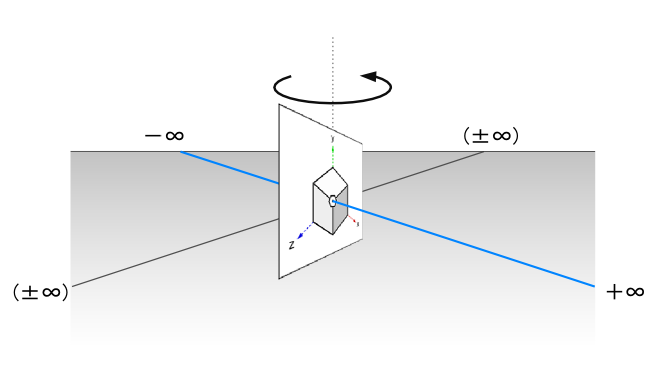
　この時に、「4次元目の軸」を回転させた時にできる平面が、「4次元平面」と言うことができます。
　これは、4次元が平面の形に落とし込まれていて、4次元より一つ上の視野がそれを見ている状態、ということになります。

　こんどは、その「4次元平面」を丸めてみます。

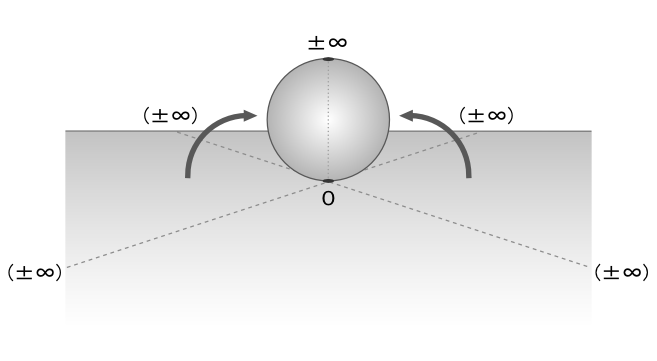
　この時にできる球が、「4次元球面」ということになります。
　これは、「4次元球」や「メビウス球」とも呼ぶことができるものです。

　これが見えている位置に「±∞」という、「前」の無限遠点と「後ろ」の無限遠点を繋げた場所があり、そこに『次元観察子ψ5』があります。
　まず、ここが「4次元対称性」が成り立つ位置 です。
　『次元観察子ψ5』は、「4次元空間」と「4次元時空」が対称性を持っている所でもあるため、「4次元対称性」は、「4次元空間」と「4次元時空」の対称性にもあたります。

　この時の「4次元目の軸」は、回転によって無数化してます。