さて、次に、「対称性」とは何か？という問題について考えてみます。
　ここでの「対称性」とは、下位の次元にある正反対の要素が、裏と表の関係のように、入れ替わり可能であることを言います。
　また、n次元対称性というのは、n次元空間から発展して見出すことができます。

　まず、「3次元対称性」とは、「2次元」の軸であるxy軸と、3次元目の軸であるz軸が、90度回転することで入れ替わり可能となることです。

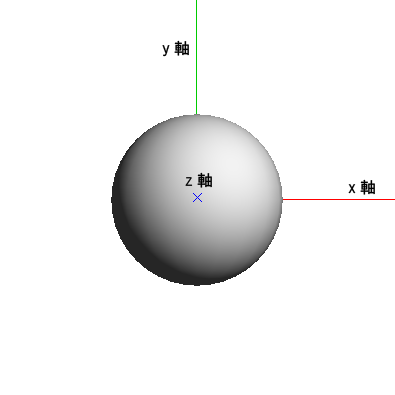
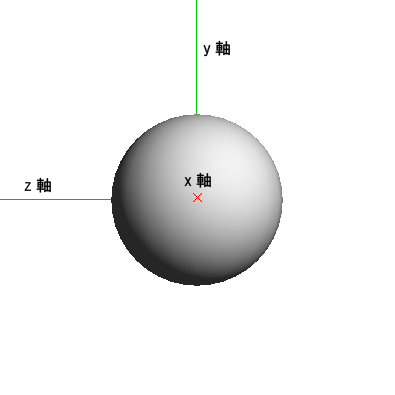
　これは、「3次元空間」での話なので、特に難しい話ではないと思います。このような座標的な物の見方は、17世紀にデカルトが発見したものであり、それ以降に発展していったものでもあります。xy軸も、z軸も、等しく「距離」であり、回転することでそれは入れ替えることができます。

　次に、「4次元対称性」とは、先ほど説明した通り、「4次元球面」にある対称性であり、それが見えるようになるためには、まず 「4次元」を発見し、今度は「4次元時空」と「4次元空間」を『等化』する必要があります。

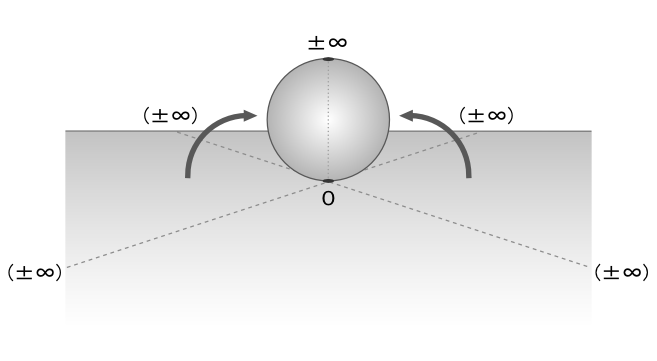
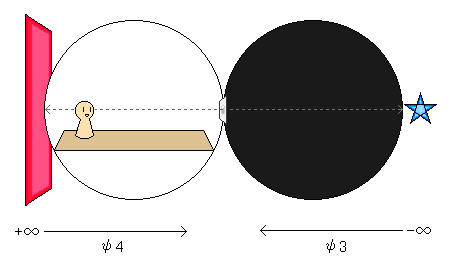
　これは、「主体」と「客体」が入れ替わる対称性でもあります。
　おさらいすると、『次元観察子ψ3』を発見することで「前」側にある『主体』が分かるようになり、そこから『次元観察子ψ4』を発見することで「後ろ」側にある『客体』が分かるようになります。
　そして、「前」側と「後ろ」側とが繋がり、それらを対象的に見る位置にあるのが『次元観察子ψ5』です。

　ここで、「4次元」がはっきりと分かるようになることで、「時間」と「空間」の対称性もはっきりと分かるようになります。
　「時間」を「空間」のように見ることは簡単ですが（時間を数直線のようにイメージすれば済む話です。）、「空間」を「時間」のように見るということが難しいです。「時間」の本質は、ベルクソンが「純粋持続」と呼んだようなものであり、それは主観的に変化するものだからです。「4次元対称性」を見出すには、こうした「純粋持続」を捉える必要があります。
　そして、「空間」の観念も、「純粋持続」のように、主観によって認識変化が起こるものだということを理解する必要があります。