次いで、ヌーソロジーでは、割と幾何学的な、ミクロ寄りな視点の世界において、『負荷』・『反映』・『等化』・『中和』という、原理的な概念があります。
　ヌーソロジーは、この『負荷』・『反映』・『等化』・『中和』の４つの原理で、あらゆる構造を捉えようとするので、これについてそれぞれ説明します。
 
〜負荷〜

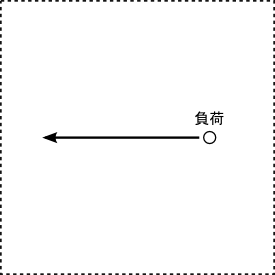
とある始原となる存在があったとして、
そこから開始する作用にあたります。
数字では、「1」に対応します。 
 

〜反映〜

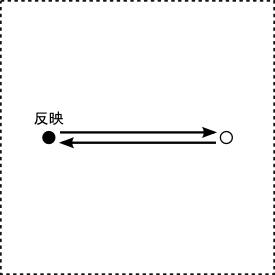
『負荷』という開始の力に対して生まれる、
それとは逆向きの作用にあたります。
数字では、「2」に対応します。
 

〜等化〜

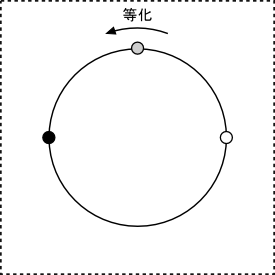
『負荷』と『反映』という、
背反するものを統合するような「回転」の作用、
または、対象性を見出す作用にあたります。
数字では、「3」に対応します。
これは、『負荷』と『反映』を、新たな次元の視点で見る力を持ちます。
 

〜中和〜

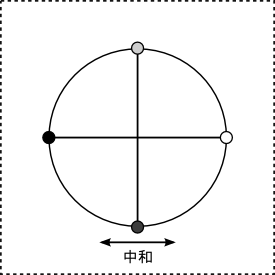
『等化』の回転に対する逆回転。
回転が相殺されるため、その意味で、『中和』は「分離」するような作用にあたります。
また、双方の対象性を見出すのを拒む作用にもあたります。
数字では、「4」に対応します。
これは、新しい物質を誕生させる力を持っています。
　
　
　これらは、『負荷』→『反映』→『等化』→『中和』と発展していく構造を持ちます。
　この４つの用語は、ヌーソロジーにおいてあらゆる所に出てくる基礎的な用語なので、押さえておくべき用語です。

　また、『負荷』と『反映』、『等化』と『中和』などは、それぞれ、「１」と「２」、「３」と「４」に対応しているわけですが、このように奇数と偶数に対応している組が作る対立関係を、『対化』と言います。
　『対化』は、それぞれを『等化』するために、必要な関係になります。

　また、これらの４つは、先程出てきた、『定質』・『性質』・『反性質』・『反定質』において、「『定質』と『性質』」⇒「『反性質』と『反定質』」という風に発展していく構造を考えると…

と当てはめることができ、それぞれの力は関係していると捉えることができます。