さて、ここで、『等化』のイメージが、イマイチなかなか付き難く、難しい所であるので、少し補足を加えます。
『等化』は、「3番目の作用として、1番目と2番目を、相互を上手く統合させるような作用である」ということですが、ひとまずそれは、「上次元の視野」によって行なわれています。
「1番目」と「2番目」を、「上次元」から見ることで、それは同一次元上にあるものと、解釈することができます。
例えば、「1番目」と「2番目」が、2次元平面場にある場合、3次元空間からそれを見ると、「同じ面にあるもの」として捉えることができます。
ヌーソロジーにおいては、これを、「対象が3次元空間上にある場合で、4次元空間からそれを見る」のようなことに、取り組むことになります。
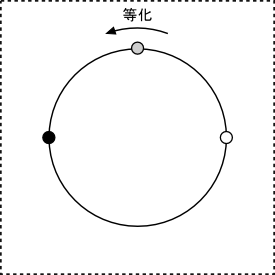
また、「円運動」にて捉えることも得策であり、以下の図においては、「新しい次元」からの円運動を捉えることによって、双方の点は、同一次元内の円心上にあるものとして捉えることができます。(以下は、1次元である線上にあったものを、2次元である円で捉えています。)
また、哲学者ヘーゲルの提唱した、「弁証法」にて説明することもできます。
ヘーゲルの「弁証法」を簡単に説明すると、まず、ある物事の提示がされた時、その提示された物事自体を、「①テーゼ(正)」と呼びます。そこから、その物事に対する問題点が指摘されるようになり、それを「②アンチテーゼ(反)」と呼びます。そして今度は、「①テーゼ(正)」が「②アンチテーゼ(反)」を取り込んで、その双方の矛盾点を解消するように、答えが導き出されます。この導き出された答えを、「③ジンテーゼ(合)」と呼びます。
このように、「①テーゼ(正)」→「②アンチテーゼ(反)」→、「③ジンテーゼ(合)」というように発展していくのが、ヘーゲルの「弁証法」です。
つまり、「①テーゼ(正)」が、まず開始した時の思想であり、「②アンチテーゼ(反)」が、その思想に対立する思想であり、「③ジンテーゼ(合)」は、対立した果てに導き出される、双方を解決するような、新たなる思想になります。
『等化』も、ここでいう、「③ジンテーゼ(合)」のようなものにあたるわけです。(加えるなら、ヌーソロジーでは④番目にあたる『中和』もあるので、またさらに新しい概念が必要になると言うことができます。)
『等化』は、実践的には、自分の精神にあるものとして、扱っていきます。
それは、説明するなら、「上次元の視野から、相反するものを統合する視点を持つ」といった所です。
お互いは違うもの同士ではあるが、ある意味では同じようなものであり、両者の差異を認めつつの共存が可能な関係です。
一方で、『中和』とは、その真逆の作用にあたります。『等化』という、上次元からの作用に対して働く、同一次元内に対して行なわれる、「相反するものを分ける」作用です。
その作用によって、相反するものは、「別々の個体」として、安置されることになります。
これは、「物質」を作る作用として、主に働いています。また、万物というのは、この『中和』の作用によって生まれていて、世界に多様な物質や生物が生まれているのは、この『中和』のおかげであるということが出来ます。
『等化』と『中和』は、今後も実践において扱う際に、また出てくる用語であるので、そうした実践の中で、理解を深めていくべきものになります。