さて、これまで『次元観察子ψ3』と『次元観察子ψ4』までについての説明をしていきましたが、これらのことがより「実践的に」理解できるように、再度、おさらいをしていきます。

　まずは、通常空間のローレンツ収縮のおさらいです。

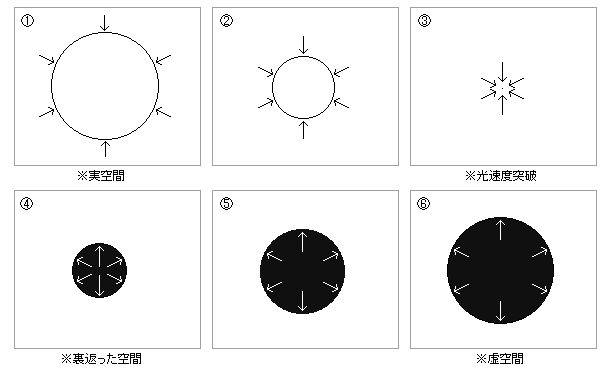
　通常空間を、無限の長さの直径を持つ球のように捉えて、どんどん収縮していくイメージを作る。そして、そのまま点の状態にして、さらに「裏返った空間」というのをイメージして、今度はそれを膨張させます。
　以上のイメージは、「全方向に対して光速度をイメージする」ということになりますが、「単一方向に対して光速度をイメージする」場合は、以下のようになります。実際に行う場合は、こちらの方がやりやすいと思います。

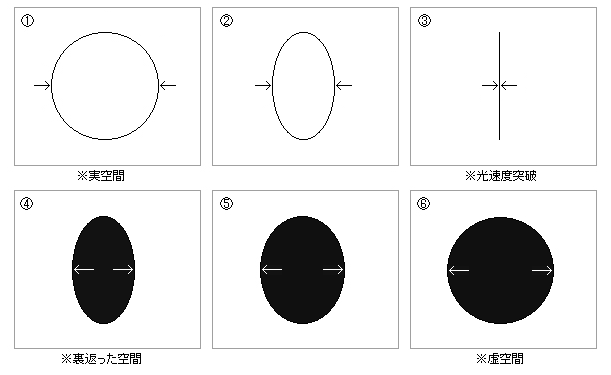
　「光速度のもの」をイメージすることと、そこから「ミクロの長さのもの」をイメージすることがポイントとなります。
　以上の行為を、フィーリングで行えるでしょうか？

　光速度以降の世界が、このようになるので、その世界をイメージする必要があります。
　恐らく、成功すると、脳に妙な負荷がかかるような感覚があるでしょう。脳の割と深層の部分か、右脳の辺りを使うでしょう。これが上手くいくかどうかは、その辺りの発育も絡んでる所です。普段の空間認識では、使わない脳の部分を、使うということになります。

　この反転を、ここでは、「基本反転」と呼ぶことにします。
　難しいとされる4次元のイメージの基礎となるので、維持が難しい場合も演習してみる必要があります。
　これが上手くいってると、次のステップへ進みやすいです。