これまで掴んだイメージをより明確にするために、「時間軸に虚数を掛ける」というテクニックを使います。これは、「時間軸の反転」を意味することでもあります。

　まず、「ある対象から放たれる光（光波）が作る球」の式について考えてみます。これは、アインシュタインの「特殊相対性理論」でも基本の式として出てくるものです。
　「ｘ, ｙ, ｚ」はそれぞれの座標、「ｔ」は時間、「ｃ」は真空中の光速度とすると、その球は以下の式で表されます。

　式の左側の「ｘ, ｙ, ｚ」には、それぞれ球の中心となる座標が入ります。式の右側はそこから放たれる球の半径であり、それは光の速度で絶大な大きさへと広がるという内容の式になります。
　現実世界において我々が「物」を認識する場合、物から反射された「光」を目の網膜が捉えて、「物がある」ということを認識します。従って、以上の式は、「対象から放たれる光を捉える」イメージだと言うことができます。
　ここで、「時間軸の反転」という概念について考えてみます。この式にある時間「ｔ」を虚数にすると、以下のようになります。

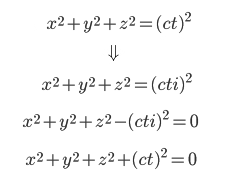
　以上の式は、「時間軸の反転」によって、「対象に向かって自身が光になる」イメージだと言っても良いのではないか？と思います。
　そして、これこそが「４次元空間上の大きさが０の球（点）」の式だと言うことができます。左側に「ｘ, ｙ, ｚ」に続く４つ目の座標変数として「ct」が追加されています。

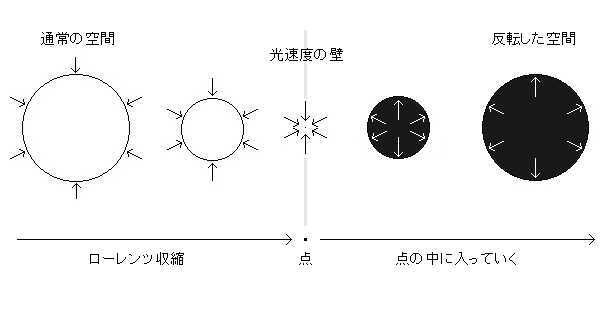
　以上の状態と、先ほどの「ローレンツ収縮」で「光速度の壁」に達した時の「点」の大きさに等しい「微小球」のイメージと一致する箇所が分かってくると、その感覚が強まってきます。

　また、「時間軸の反転」とは、「ベルクソンの『純粋持続』について」の項目で説明したように、時間を「純粋持続」として捉えることであると、解釈することができます。
　ベルクソンは、アインシュタインと同時期に活躍した哲学者であり、時間の考え方が正反対であったことも有名ですが、ベルクソンの捉えた時間は「反転した時間」であると解釈すると、色々と辻褄が合うことになっていきます。

　それから、アインシュタインの特殊相対性理論によると、「４次元時空」は、「ミンコフスキー時空」として説明されます。「ミンコフスキー時空」とは、物質が光速度に近づくことにより、時間や空間に歪みが生じる時空のことを言い、「ｘ, ｙ, ｚ」に、「ｃｔ」を加えた4値で構成されるものですが、アインシュタインの言う時空像においては、この中で「ｃｔ」のみ特別扱いとなります。
　しかし、この「ミンコフスキー時空」における「ct」に「虚数」が入り込むことによって、「ｃｔ」も「ｘ, ｙ, ｚ」のように「空間軸」と同様に扱えるようになり、反転した「ｃｔ」が４次元目の軸となり、「４次元空間」としての式が成り立つようになります。
　つまり、「時間軸の反転」は、「４次元時空」⇒「４次元空間」へと変換する力を持っているのだと言うことができます。

　この辺りの感覚を併用して掴むことで、「反転」の感覚がより顕在化してくることでしょう。