次に「無数化」です。
　これは、「『負荷』側を数え切れないぐらいたくさんにする。」ということです。
　今回の場合は、『次元観察子ψ3』を構成する『主体』を「無数」の数にすることになります。

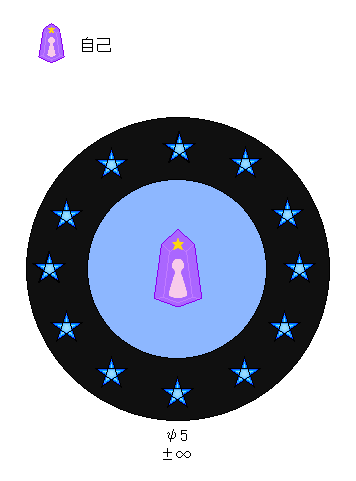
　上記の図のように『主体』が無数になった位置に、『次元観察子ψ5』と、それに対応する『自己』が存在します。

　そもそも、『主体』と『客体』を「回す」とはどういうことなのか？
　それは、『客体』を『主体』に塗り替えるということになります。
　『客体』を『主体』に塗り替えるとはどういうことなのか？
　『客体』というのは、無数の数で存在しているものである・・・つまり、『主体』を『客体』のように無数の数にすることが、『主体』で『客体』を塗り潰すことにあたります。
　「回転」とは、それを可能にする行為になります。

　また、逆に、『主体』を無数にすることが、「回転」と同じことを意味するということでもあります。