不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
◆◇垂子の無数化◆◇
前回は「回転」について説明した。
次は「無数化」についてである。
『次元観察子ψ3』の時に「無数化」が出てきたように、
『次元観察子ψ5』の時にもこれが出てくる。
・・・というかそもそも・・・
これについては「回転と無数化は同義。」というような理解の仕方をして良い。
「回転」は、アニメーションのようにたくさんの視点があって成立するのである。
Kitcat実験でもそうだった。

一般的に放映されているアニメーションのイメージもそんな感じ?と言えそうだが・・・
ただ、難しいのは、ヌーソロジーの場合は直線的な時間を流れるようなアニメとは違うことである。
アニメはパラパラ漫画のように時間とともに次の絵に進む仕組みだが・・・
我々の実際の知覚は「今」が連続しているだけである。
この違いが分かるだろうか?
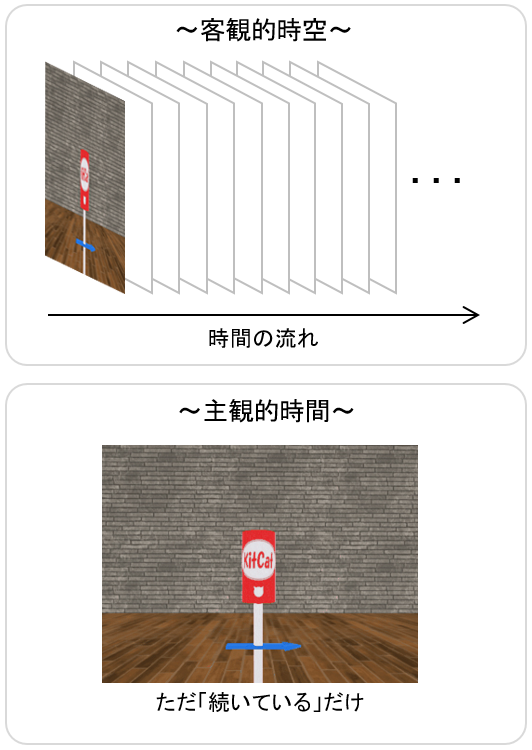
以下のような「Kitcat実験のアニメーション」の場合は、
「常に一瞬一瞬の今がある」という感じで、「無数の知覚正面」があることで成り立っている。

あちこちの方向へ無数化
さて、「無数化」ということで、奥行き方向が無数化してあちこちの方向になっている状態もイメージしてみよう。
これもまずは「知覚正面」を意識して・・・
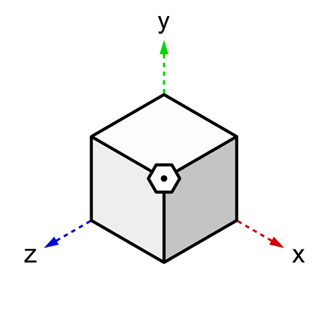
それを色んな方向へあちこちに動かしてみる。
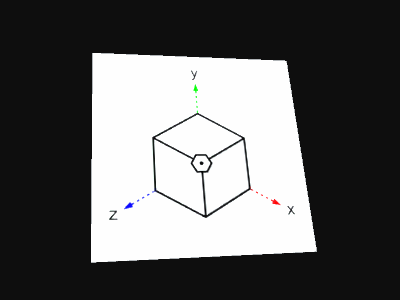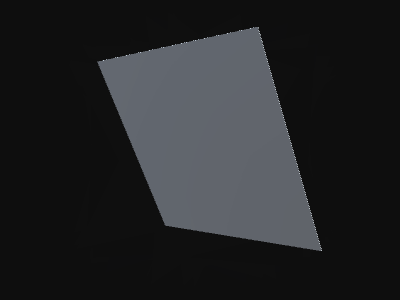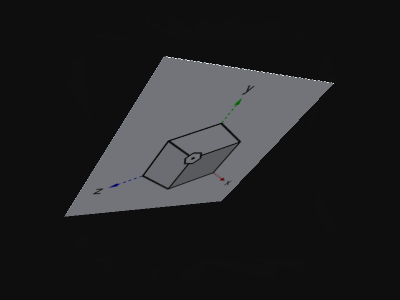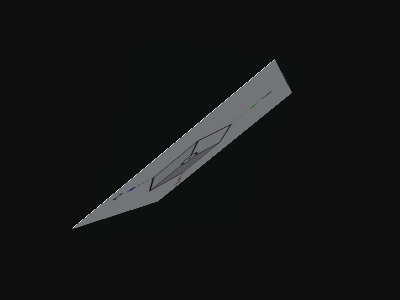
上記のアニメーションは比喩なため、時間の経過によってあらゆる方へ向かうようになっているが・・・
ψ5の場合は「同時に色んな方向にある」みたいな感覚に近い。
これもなんとなくψ5の方向に近づいていけるんじゃないだろうか?
無数の主体
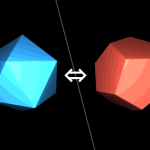
さて、次に『主体』を無数にしてみる。
次元観察子ψ3の場合は以下のように一個の主体があるわけだが・・・
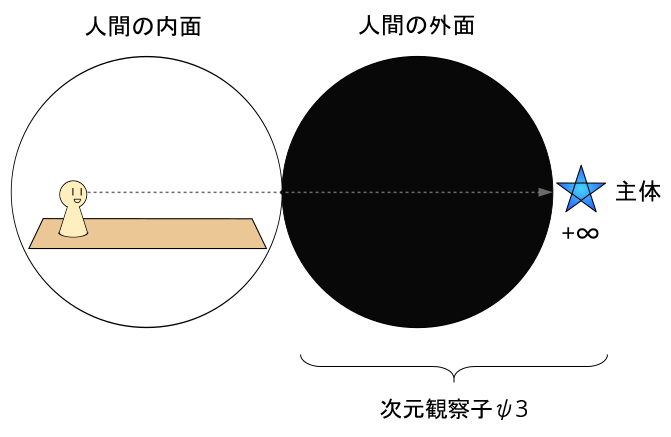
次元観察子ψ5の場合はどうなるのか?
次元観察子ψ5が顕在化すると、以下のように無数の主体が周りにあるような感覚になる。

前回の「回転」の説明と合わせて、そうした感覚が分かるだろうか?
これが分かってくると「ψ3とψ4の等化」も分かってくるし、
ヌーソロジーに関する色んなことも分かってくるので、
地道にやってみよう。
↓続き
|
2013:The Day God Sees God 人類が神を見る日 [ digital edition ]
ヌーソロジーをちゃんと学習するならこれ! |