不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
引き続き、『次元観察子ψ5』に絡んだ話である。
今回はヌーソロジーの基礎として重要な概念の一つである
「３次元球面」についての説明をしていこうと思う。
「２次元球面」とは何か？
まず、早速「３次元球面とは何か？」を説明していきたい所だが・・・
それをいきなり説明しようとしても難しいので・・・
先に「２次元球面」の話をしようと思う。
２次元球面は単純なもので、基本的にごく普通の球をイメージしてもらえば良い。
2次元球面は普通の球に近いものであるが・・・正確に言うと「球」ではなく、「球面」と書いてあるように、ごく普通の球の周りにある面のことを言う。
例えば、テニスボールをイメージすればそこに２次元球面があるし、地球儀をイメージすればそこにも２次元球面がある。
このように、２次元球面は２次元のものを球面にはりつけてできたものに該当する。
これをもっと分かりやすく説明すると・・・例えば以下のように普通の「紙」があるとしよう。
平たい紙は２次元の形をしている。
それをテニスボールに包んでみよう。
この時、テニスボールを包む形になった面が２次元球面になるわけである。
そこまで難しい話ではないと思うので、分かっただろうか？
そして、２次元球面は３次元の球の形で存在しているので・・・
２次元球面は３次元空間に存在するものと言うことができるわけである。
つまり、n次元球面は(n+1)次元空間に存在するという原理があることを、まずはよく覚えておこう。
「３次元球面」とは何か？
次に「３次元球面」についてである。
これを簡単に説明すると、２次元のものを丸めたのが２次元球面なので・・・
３次元のものを丸めたのが３次元球面ということになる。
それはどういうことか？を理解するのにまず必要なのは、『「知覚正面」を平面として空間を見る』の話である。
以下の「エルンスト・マッハが左目で観た視覚体験」のように、３次元空間を平面として捉えことをやってみよう。
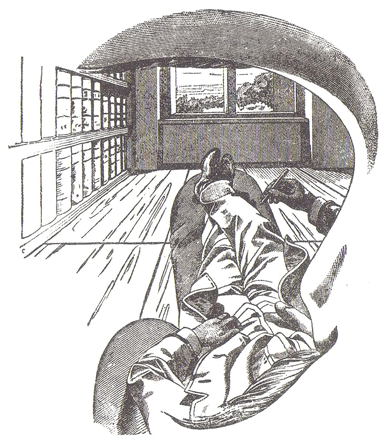
そして、実体は３次元空間であるそれをもし球状にすることができれば・・・
「３次元のものを丸めた３次元球面」ができるわけである。
また、以下の「４次元を発見するための図」も同様である。
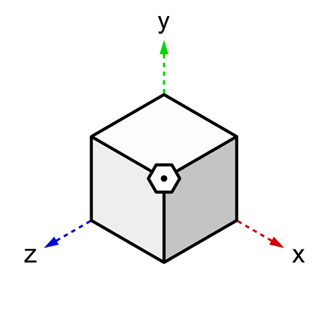
これも立方体を平面に落とし込むことを表現した図なので、それを球状にすれば３次元球面ができるはずである。
それから、２次元球面の所で説明した「n次元球面は(n+1)次元空間に存在する」という原理を踏まえると・・・
３次元球面は４次元空間に存在するものということになる。
したがって、３次元球面を理解することは、４次元空間を理解することと同義である。
以上の説明で３次元球面についてが分かっただろうか？
・・・いや、正確には分からないかもしれないが・・・理屈としてはそんな感じである。
３次元球面をさらにつきつめる
３次元球面をもっと分かりやすくするために、以下の「４次元を発見するための図」をベースに考えていこう。
これを以下のようにペタっと平面に張り付けてみよう。
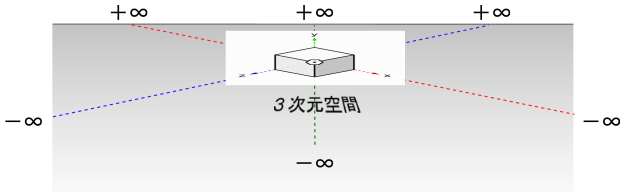
上記で張り付いている所は図だと平面のように見えるが、x・y・zの軸を持った３次元空間である・・・ということを前提として認識しよう。
そして・・・その空間を丸めてみよう。
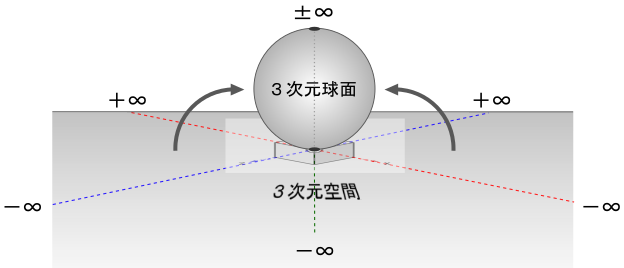
すると、一番上の部分は、前側の無限遠点（-∞）と後ろ側の無限遠点（+∞）が繋がった±∞の位置になる。
±∞の位置には『次元観察子ψ5』があり、これは『等化』を表すカタチでもある。
したがって、３次元球面が分かる位置が『次元観察子ψ5』の位置であるため、３次元球面はψ5を理解するためのカギとなるわけである。
さて、ここで半田広宣さんの公式ブログの内容を参照してみよう。
以下の『4次元を認識するときの心得』という記事にも３次元球面についてが書かれている。
自分を3次元から出す、つまり、3次元として見えている世界を視野空間の中に見るなら、それを見ている主体自身は3次元から出ることができているということだ。このとき3次元空間は3次元球面と化す。この3次元球面が見えたとき、私は絶対不動の私となる。不動明王のようなものである。
ここで出てきた「不動」というキーワードは、前回『「不動の自分」を掴む感覚』の項で出てきた不動の意味と同義であり、『次元観察子Ψ5』とそれが関係しているわけである。
「３次元球面」が分かるとここに書いてあるテキストの意味も分かるはずなので・・・
頑張って理解してみよう。
（続く）
