不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
これまで『次元観察子ψ5』の認識方法について色々と説明してきたので・・・
ここで、そのやり方のおさらいをしよう。
これまでのおさらい
ゴール
まずは、ψ5を発見することのゴールについてである。
前提として、以下のように『人間の外面』と『人間の内面』があり…
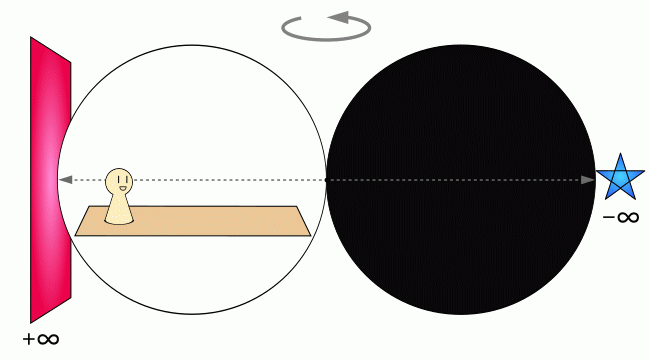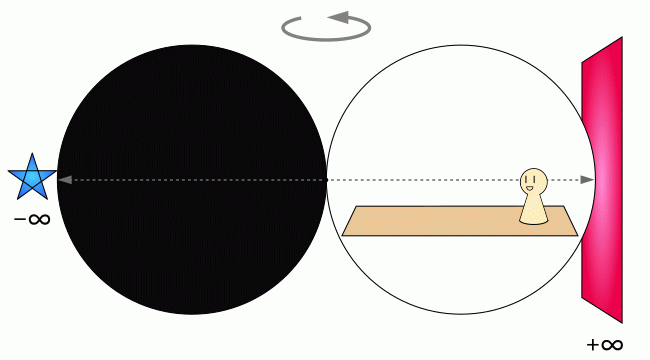
前側の無限遠点[－∞]と、後ろ側の無限遠点[+∞]がある。
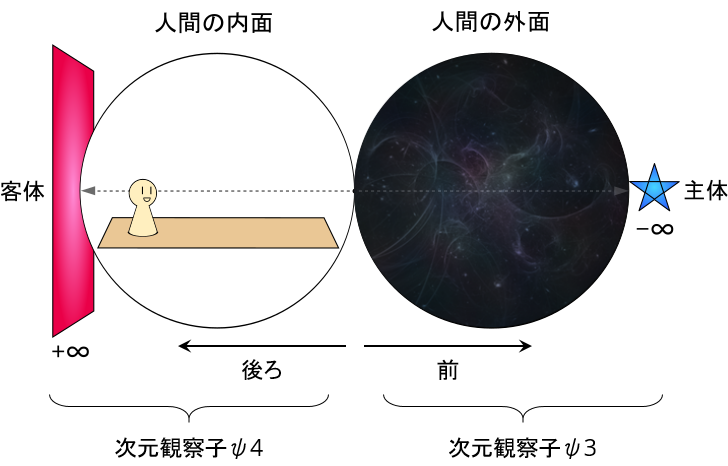
そして、その前と後ろが繋がった場所に『次元観察子ψ5』がある。
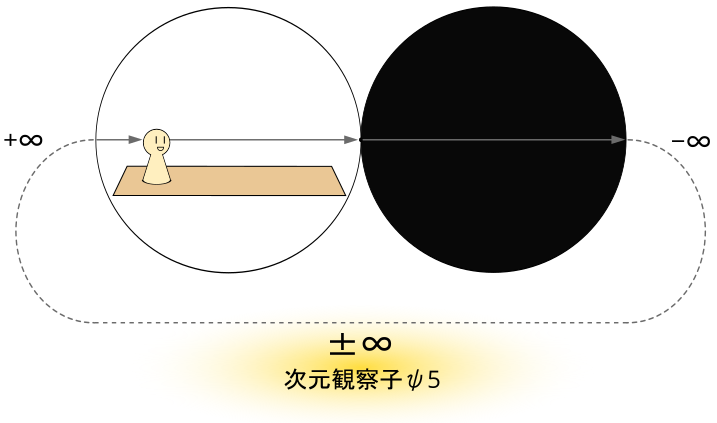
これが分かることにψ5のゴールがあるので、まずはそれを基本として忘れないようにしておこう。
回転
そして、そのための理解の秘訣の一つが「回転」である。
これを理解するために、まずは『垂子』を理解する必要がある。
『垂子』は『次元観察子ψ3』が分かった時に分かるもので、端的に言うと以下の「4次元目の軸を発見するための図」の垂直方向にある線と思ってもらえれば良い。
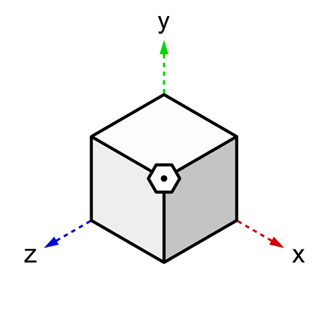
そして、4次元の感覚が掴めている状態のまま・・・これを回転させる。
簡単に説明してみたが・・・どういう意味かをよく理解した上でこれをやっていこう。
それから、以下の図のアニメーションのように、回転のイメージを強引に作ってみたりするのも良いかもしれない。
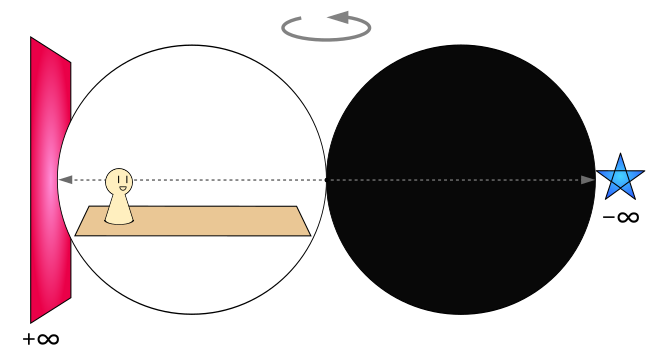
さらに、この「回転」はKitCat実験を意味するものでもあるため、それについても復習しよう。
無数化
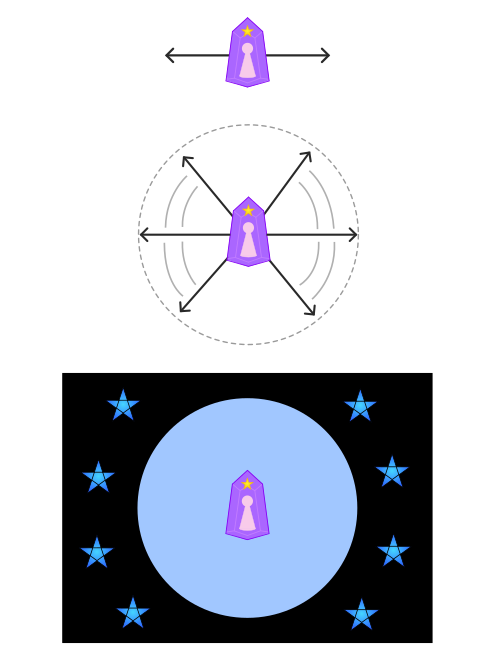
次に重要な概念は「無数化」である。
無数化は「数えきれないほどたくさんになる」みたいな意味だが・・・
これをψ5に適応した場合を分かりやすく説明すると、「4次元目を発見するための図」を無数の方向にするようなイメージになる。
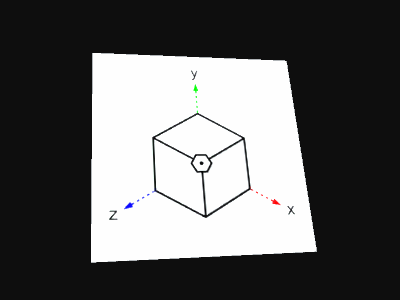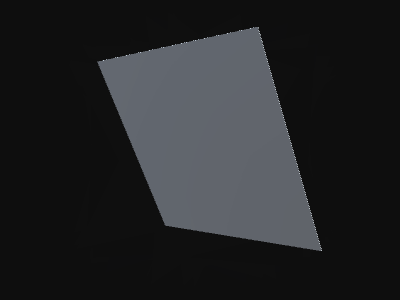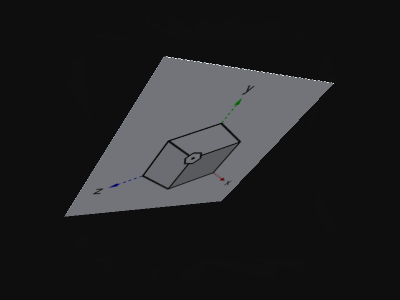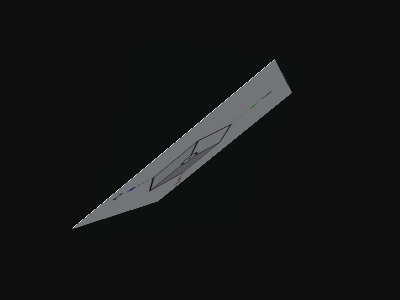
『垂子』を「光の線」のようにした場合は、以下のようになる。
「無数化」が成功すると、無数の主体に囲まれた所にΨ5があるイメージになる。
以上のイメージが分かれば、『次元観察子ψ5』もなんとなく分かってくるだろうと思う。
裏返し（強引に反転させる）
次に『「二重反転」をやってみる』の項で説明した反転方法である。
こうして強引に反転させることを「裏返し」と呼び、二重の裏返しをやってみよう。
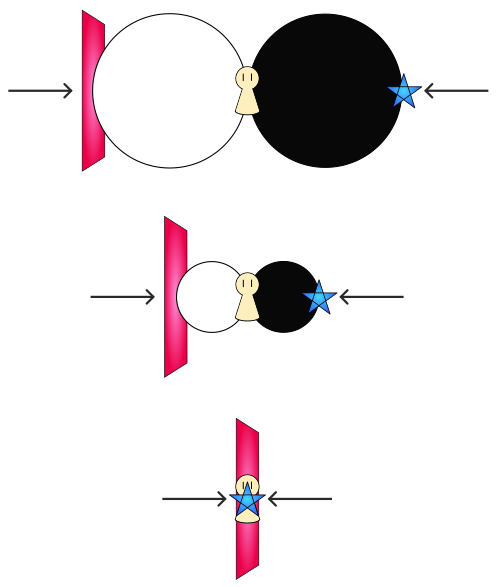
実は、筆者（Raimui）自身がこれを思いついた時、一番強烈な体感みたいなものがあった。
他の人はどうなのだろうか？
分かると強烈なのでやってみて欲しいものである。
不動の自分
『次元観察子ψ5』は「不動の自分」が分かる位置であるため、それが分かるようなワークをしていくこともψ5の認識方法になる。
以下のような「眉間鉛筆」のワークをやったりしてその感覚を掴んでいこう。
これは「ψ5の認識方法」というより「ψ5のゴール」の話に近いが・・・
こうしたゴールがイメージできるようになることが認識方法にも繋がっている。
３次元球面について理解する
最後に「３次元球面」の理解である。
前回の項でそれについて説明した。
これをイメージすることは割と難易度が高いかもしれないが・・・
ヌーソロジーを本格的に理解するための概念としておさえておこう。
「構造」と「カタチ」を理解することの意義
・・・以上。
これまで説明してきた「次元観察子ψ5を構造的に理解するための話」に関しては上記の通りだったと思う。
ヌーソロジーで肝となるのはとにかく「構造を理解すること」であり、その構造は言い換えると「カタチ」とも言える。
それらを理解するための作業は地味かもしれないし、こうして説明する作業も地味かもしれないが・・・
これが分かると強い「確信」と「体感」が生まれ、強く明確でスピリチュアルな（精神的な）力になる。
また、その道を進んでいくとただの感覚的なスピリチュアルの力だけでなく、知性的な力も同時に身につき、地に足の着いた思考もできる。
そして、その構造が理解できたら、今度はそこから派生してもっと色んなことが分かるかもしれない。
社会の話、エンタメの話、芸術の話、文明の話、宗教の話、心理の話・・・・それらはつきつめるとすべて「自己」の話にも繋がるし、「他者」の話にも繋がる。
「ψ5の構造」の話をしっかりと踏まえると、「自己」について掘り下げていくこともやりやすくなるため、自己探求のためにヌーソロジーを学ぶ意義は大きい。
そのため、そうした話を深めるために、ここではあえて構造の話を徹底しておくのがこのシリーズのコンセプトである。
以上を踏まえて、『次元観察子ψ5』の話とそれに絡んだ話をもう少し続けていこう。
（続く）
