不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
◆◇ψ7を認識するために(前編)◆◇
↓前回
「前編」だった前回に引き続き、『次元観察子ψ7』の具体的な認識方法についてを説明していく。
自己の無数化
まず、『等化』の基本は「回転」と「無数化」である。
これは『次元観察子ψ5』の時もそうだったし、『次元観察子ψ7』の時もそうである。
ψ5の時は、ψ3を構成する「主体」が無数にあった。


ということは・・・ψ7はψ5を構成する「自己」が無数にあるイメージで良いのではないだろうか?

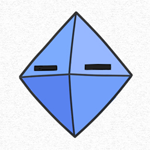
また、それら無数の自己にはそれぞれの「前」があり、その真ん中に「モノ」がある仕組みになる。
そのため、ここで「モノ」がある位置に存在するのが『次元観察子ψ7』に該当する。
![]()
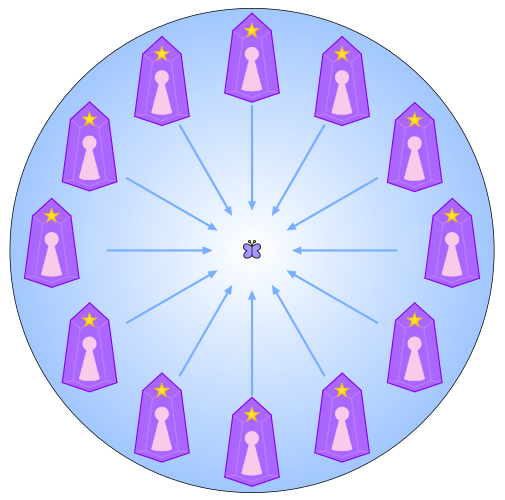
ヌーソロジー公式では、以下のような図で説明されている。
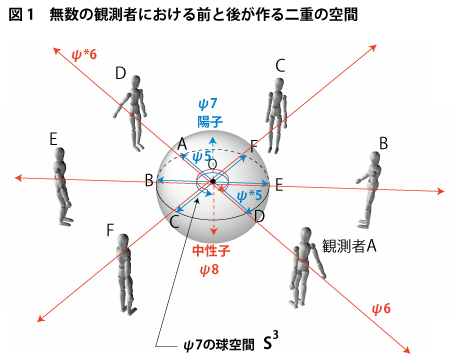
それから、この時に生じる「球」が重要であり、『次元観察子ψ7』のことはヌーソロジー用語で『球精神』とも呼ばれている。
おさらいすると、ψ3は『垂子』→ψ5は『垂質』→ψ7は『球精神』・・・といった構造になっているため、それぞれのキーワードを覚えておこう。
自己球体の無数化
次に、自己が無数化する様子を試しにアニメーションで作ってみよう。
自己には以下のような3次元球面があるとする。
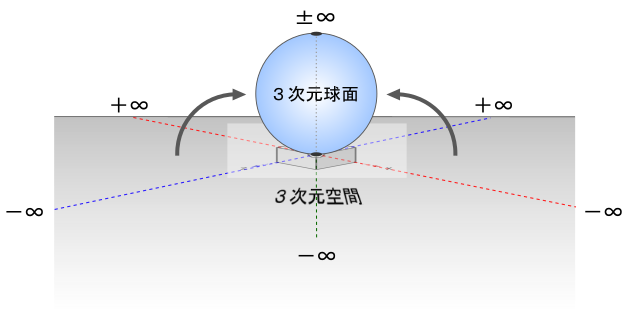
3次元球面はこうしてみるとただの球だが、3次元空間からの次元上昇のため「回転」を含んでいることを踏まえておこう。

それを無数化して、また一つの球にまとめてみる。

この無数化表現はあくまで比喩だが・・・
これを「無数の状態を重ね合わせて持っている」というように捉えることができると良い。
このように、「無数化した自己」がモノになっている時の意識が、ψ7の位置になるわけである。
背中合わせの状態からの回転
最後に、前回説明した「背中合わせの自己と他者」と自己球体の回転のアニメーションを組み合わせてみる。
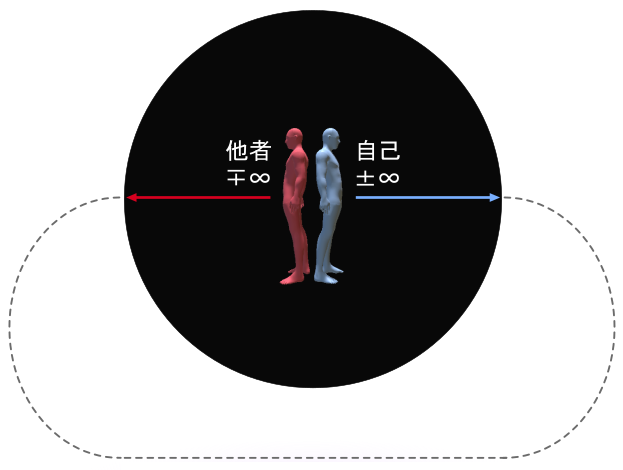
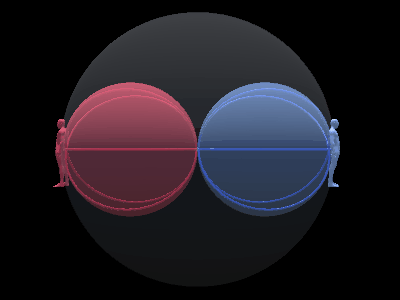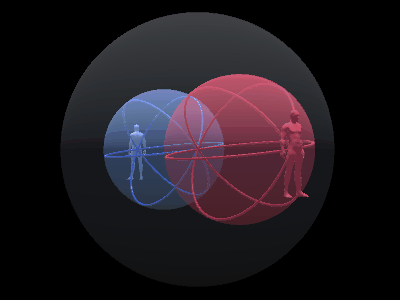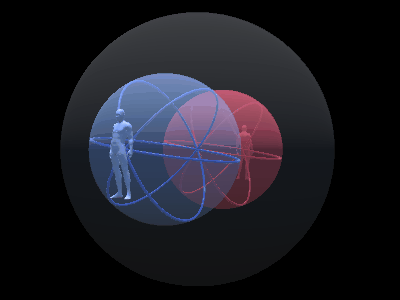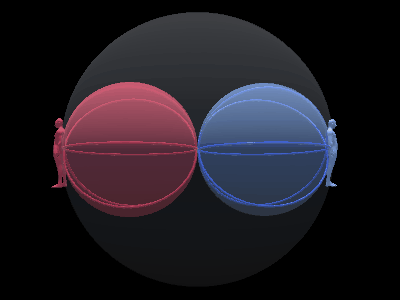
このアニメーションは非常に奥が深い。
これの意味が分かるだろうか?
ちなみにこれは『2009-2010年ヌースレクチャーDVD Vol.7』で説明された表現の再現である。

disk1:メビウスの帯と次元観察子 / disk2:元止揚空間の幾何学
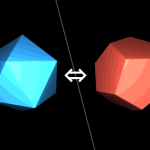
簡単に説明すると、自己と他者があって、青い球は自己側にある3次元球面であり、赤い球は他者側にある球である。
それがさらに回転していて、双方を『等化』するようになっている。
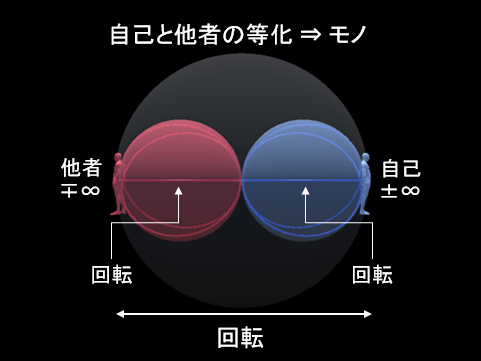
こうした構造から、ヌーソロジーで「モノ」と呼ばれる存在が生まれるわけである。
また、ここで自己側と他者側の回転方向について注目してみると・・・
自己の後ろについている球は左回転、他者の後ろについている球は右回転になっている。


ただし、球の中心より逆を向いてる自己自身と他者自身から見た場合、自己には右回転があって他者には左回転がある。
(ちなみにこれは、仏教で悟りや吉祥の象徴として用いられている「卍」と、ナチスが政治的プロパガンダとして使った「ハーケンクロイツ」の形ともそれぞれ一致する)




自己側には右回転があって、他者側には左回転がある!
逆方向から見るとそれらは逆の回転に見える!
この回転方向も重要なキーポイントなため、覚えておこう。
そして、この「自己✕他者」の構造からヌーソロジー的な「モノ」が生じるわけだが、この構造をもっと外側から見ていった場合・・・
通常の人間型ゲシュタルトを持った「自我」からそれを見ると、それはただの物質として見えるようになっている。
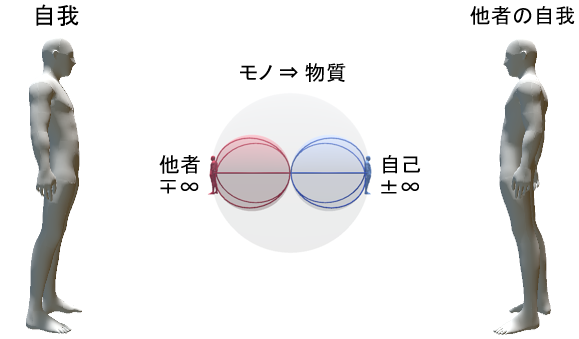
この意味も分かるだろうか?
この辺りの構造は『次元観察子ψ7』の核心的な所なので、これが理解できるようになると良いと思う。
・・・以上。
『次元観察子ψ7』の構造のポイントとなる所をざっくりと説明してきた。
これらはまだまだ深堀りできる話だが・・・
これだけのポイントでも大体の理解はできると思う。

『元止揚』における最終到達地点である『次元観察子ψ7』は、自己と他者の『等化』や、『位置の変換』といったワードが出てくるものだが・・・その意味はかなり深い・・・
人間の世界より大分離れた、本格的な高次元の世界への入り口となっている。
『次元観察子ψ7』が分かった時の意識は、『次元観察子ψ3』が分かった時のインパクトや、『次元観察子ψ5』が分かった時のインパクトよりもまた強烈かもしれない。一層違ったものになるだろう。
ψ7に絡んでくる「自己と他者の等化」は、その意識進化の中で無数の他者をも巻き込んでいくものになるかもしれないし、「モノの創造」もまた壮大な意味を含んでいることである。
それは神々をも巻き込んだ壮大な話になるかもしれないため、そんな感覚もやってくるかもしれない・・・
↓続く
|
2013:The Day God Sees God 人類が神を見る日 [ digital edition ]
ヌーソロジーをちゃんと学習するならこれ! |