
不定期連載『サイキックの研究と分析』シリーズ。 記事一覧はこちら。
◆◇「オイラーの公式」についてと数学の話◆◇
今回は数学の話をしましょう。
「オイラーの公式」というのがあります。
このオイラーの公式はリチャード・ファインマンという物理学者が、
「すべての数学のなかでもっとも素晴らしい公式」とか言ったとかなんとか、
それが有名なぐらい有名な公式です。
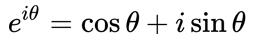
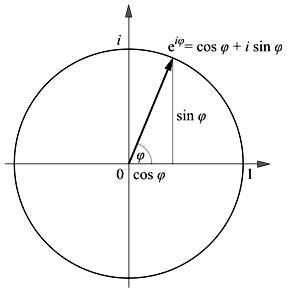
以前出てきた「波動関数」の式でもオイラーの公式がでてきます。
量子力学はオイラーの公式が中心にある・・・これはポイントなので押さえておいてください。
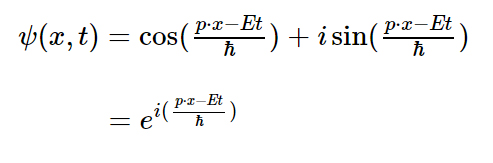
あと、「オイラーの公式」には「虚数:i」が使われています。
この「虚数」もサイキック解明において重要であるし、
sinとcosがあるということで「波」の式になってる所も重要です。
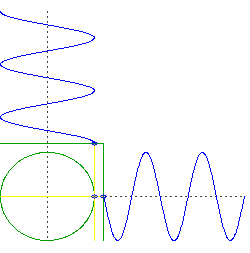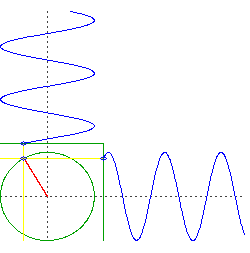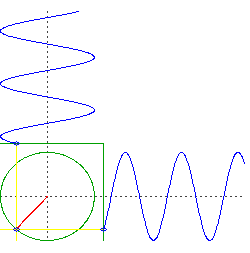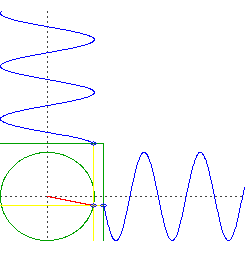
Math Gifs – Album on Imgur
以上の図は、あくまで実数の世界をぐるぐるしてますが、
「実数の軸と虚数の軸をぐるぐるしている」のがオイラーの公式です。
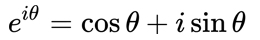
・・・と言っても、なんだかよく分からないかもしれませんが・・・
とりあえずはなんだかよく分からない概念のものとぐるぐるしている程度に思っといてください。
それから、オイラーの公式は「オイラーの等式」が成り立つという素晴らしさがあります。
オイラーの等式は以下の式です。
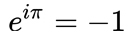
自分は高校時代、それなりな数学好きであったので、
これを見て「まじで!?」と「なんで!?」という衝撃はありました。
高校数学がある程度わかっているとそうなります。
分かりやすく言うと、πの近似値は「3.14…」、eの近似値は「2.718…」です。
あとは2乗するとマイナスになる概念である「虚数:i」。
それぞれ別の分野から出てきた数字ですが、
eをiπ乗すると、何故か「-1」ですっきりまとまるという謎の式です。
これが成立する理由はオイラーの公式にあって、
オイラーの公式のθの値にπを代入すると・・・確かにこの式が成り立ちます。
オイラーの等式は、「i」や「π」や「e」といった、
一見関係のない定数や虚数が関連性を持つことが分かったという、
数学者や物理学者にとって不可思議なものともなりました。
オイラーの公式に絡んだ数学の分野は「三角比」「指数・対数」「虚数」「微分・積分」あたり。
これを理解するだけでも高校数学はやる価値があるのだろうと個人的に思っている重要概念・・・・・・なんだけど、
詳しく書いていくと地味になりそうなネタなのでこの辺にしておきます。
「オイラーの公式」については以下の本などに書いてあります。
ということで、脱線はするものの、「数学」もサイキックを扱う上で絡めて欲しい分野です。
これは、「よく分からないものを扱うからこそ、逆に論理的な知性が必要」という話にもなります。
「原理原則から理解する」ことが「サイキックの理解」に必要という話にもなります。
今はインターネットが発達しているので、何か面白い数学ネタでも見つけて、
それと絡めて自分の気になるジャンルの数学を学んでみるのが良いでしょう。
数学を学ぶのには学校の授業とかは絶対必要というわけではなく、
モチベーションさえあれば独学でなんとかなる学問です。
(分からない所を質問したら答えてくれる人とかはいた方が良いですが。)
■次へ





















にわかには分からない素朴な数学の謎について書いてみます。
∞(無限) ÷ ∞(無限)=1
1 ÷ 無限小 = 無限大
8 ÷ 8 = 1
4 ÷ 4 = 1
0 ÷ 0 = 1?
1 ÷ 0 = ?
0で割るのは「割っちゃいけない」と言われてるのは有名な話ですが、
解釈するなら無限大でありマイナス無限大でもあるみたいに捉えることができます。
tan90度がそれと同様です。
0÷0はまたよく分からないですね。先頭に0があるから結果も0かもしれません。