不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
◆◇実数と虚数の付随イメージ◆◇
前回の複素空間モデルの話でも出てきた「オイラーの公式」。
ヌーソロジー学習おいても重要なため、たまに出てくる。
![]()
これは物理学者のリチャード・P・ファインマンが、
「我々の至宝」や「すべての数学のなかでもっとも素晴らしい公式」と言ってたこともある。
そんな異名を持つすごい公式である。
数学的には「オイラーの等式」に変化するということで、数学好きの間では人気が高いと思う。
![]()
しかしながら、以下のような数式と図は・・・
![]()
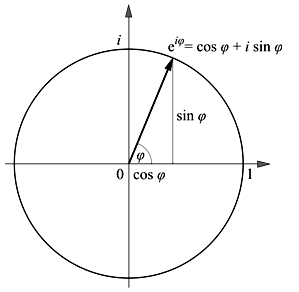
なんとも簡素であり・・・
数学が苦手、数学アレルギーみたいな人にはよく嫌われる。
そこで、「イメージで捉えてみるとどうなるだろうか?」ということを今回やってみようと思う。
虚軸と夜、実軸と昼
前回説明した「複素空間モデル」によると・・・
虚軸は『人間の外面』の方向であり、実軸は『人間の内面』の方向である。
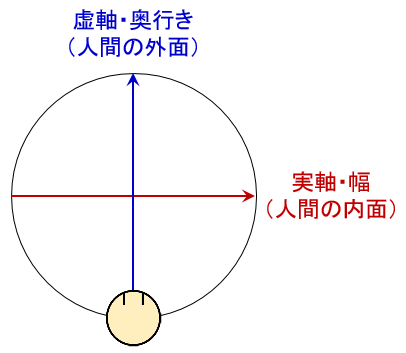
また、『夢の世界のビジョン』の項で説明したように
『人間の外面』は夜に対応し、『人間の内面』は昼に対応するとされている。
OCOT情報も、昼と夜は「対化」の表現だと言っていた。昼は人間の内面で、夜は人間の外面の現れだってこと。確かに、人間は昼間は客観世界(延長)の中で生き、夜は主観世界(持続)に生きるのが基本。これは表相が等化された世界と、表相を中和した世界(表相の等化を無効にする)の関係と言っていいかもしれない。
そこで、夜と昼は、それぞれ以下みたいなイメージとしよう。


そうすると、虚軸と実軸はそれぞれ以下のイメージに向かうことになる。
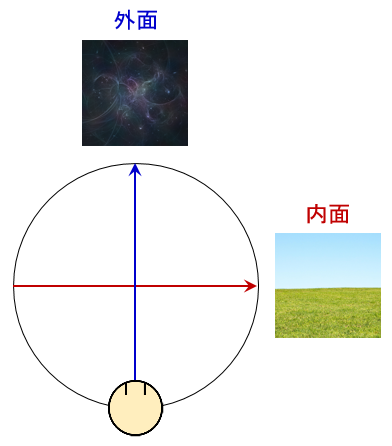
オイラーの公式に当てはめてみる
それから、以下の式はどんなことを意味するか分かるだろうか?
![]()
まず、これは「関数」になっているので、
「xの値にナニカを入れると、ナニカの値を返す」
ようになっている。
そして、その値は「複素数」として返ってくる。
複素数とは「実数と虚数が合わさったもの」なので、この関数のxに値を入れると、「実数の値がいくらかと、虚数の値がいくらか」が返ってくるわけである。
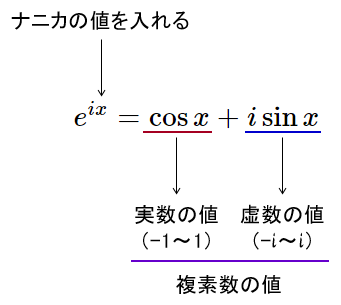
例えば、実際に値を入れていくと、以下のようになる。

ちなみに、sinやcosにはラジアンの値を入れるものなので、一般的には以下のような値が想定される。
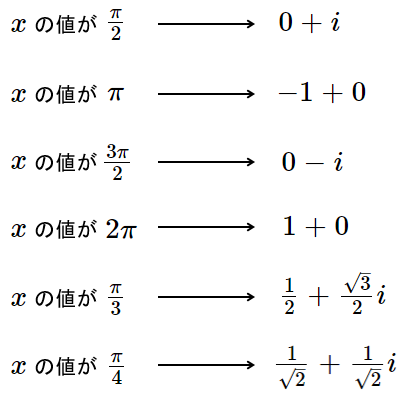
xにランダムな値を適当に入れてみた場合、その結果の値をCGにして表すと以下のようになる。
紅色の点の位置が実数の値、蒼色の点の位置が虚数の値。
白線の位置が0で、それより上がプラス、それより下がマイナスの値とする。

それから、xの値をだんだんと増やしていった場合、以下のような動きになる。

面白いことに規則的な動きになるのが分かるだろうか?
「オイラーの公式」で出した二つの値は、複素平面の円周上の値に必ずなる。
したがって、実軸と虚軸からなる複素平面があった場合、オイラーの公式は円周上をグルグル回るように値が変化するものになっている。

数学が苦手な人向けに説明したが、だいだい分かって来ただろうか?
そして、実数の世界を昼、虚数の世界を夜のイメージとすると・・・
先のアニメーションは以下のようになる。

画像生成AIを用いたイメージ
あと、画像生成AIを用いて、以下のようなイメージも作ってみた。

「オイラーの公式」について、このようなイメージができることが何となく分かっただろうか?
オイラーの公式と波。エーテル体と回転
また、オイラーの公式はsinとcosで構成されているため、「波」のようにもなっているわけである。
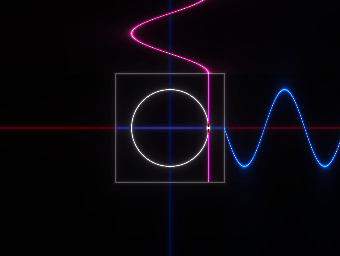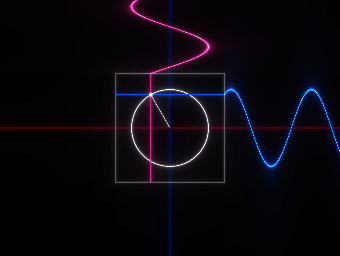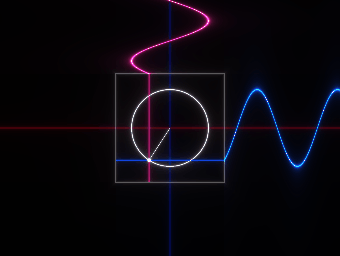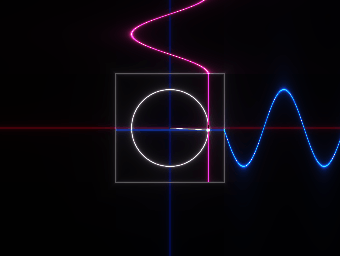
量子力学で実際に出てくる式は以下のようなものだが・・・
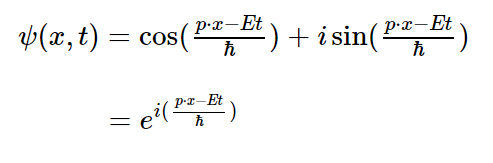
そこでも「オイラーの公式」と「波」のような構造が出てくるから、
「波動関数」と呼ばれている。
あとは、虚軸は「エーテル界」とも言われているので、エーテル体っぽいイメージでも良いかもしれない。
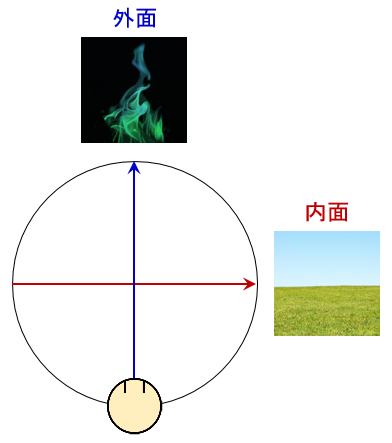

このように、「オイラーの公式」というとなんだか数学が苦手だとイメージしずらいかもしれないが・・・
とりあえず「回転」と「行ったり来たり」の動きが大事なわけである。
なんとなく伝わっただろうか?
↓続き
|
2013:The Day God Sees God 人類が神を見る日 [ digital edition ]
ヌーソロジーをちゃんと学習するならこれ! |