
不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
◆◇複素空間モデル◆◇
『次元観察子ψ3~ψ4』についてこれまで色々と説明してきた。
その中で、以下の図はヌーソロジーを学習していた当初の自分(Raimu)がヌーソロジー理解のために使っていたオリジナルのモデルである。
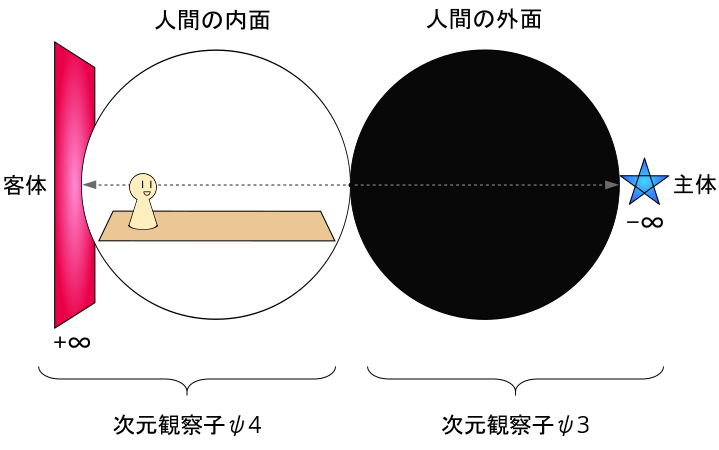
自分は長いことこれで理解していたし、今でもこれをベースにした学習をしている。
ある程度はこれでどうにか理解することもできると思う。
しかし、ヌーソロジーでは別のモデルとして「複素空間」を使ったものもあるため、
今回はそれについて説明していこうと思う。
複素空間モデル
複素空間を使ったモデル・・・即ち「複素空間モデル」とは何か?
ヌーソロジーで以下みたいな図を見たことあるだろうか?
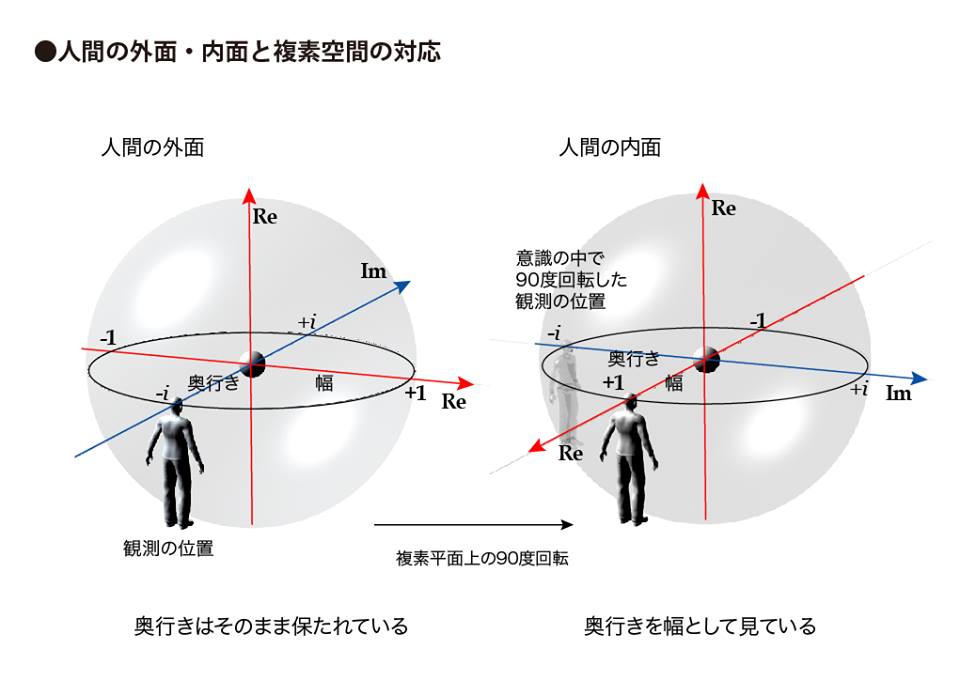
【ヌースの基本概念】人間の外面・内面と複素空間 – cave syndrome
これはヌーソロジーで行う認識を複素空間に対応させてできたものである。
既に2005年ぐらいからベースとなる考えはあったみたいだが、『2013年ヌーソロジーレクチャー』シリーズでちゃんとまとまるようになった手法であるため、2013年から積極的に使われるようになった。
これに近い図は2009年に出版された『2013:人類が神を見る日』のAdvanced Edition版の時から描かれている。
(書籍の最後の方。DL版だと443ページより引用)
『2009年ヌーソロジーレクチャー』シリーズでも次元観察子ψ3~ψ4や変換人型ゲシュタルトの説明はあったが、『2013年ヌーソロジーレクチャー』の説明ではだいぶ内容が違っている。
そのため、変換人型ゲシュタルトそのものの内容も変わったように見えるかもしれないが、「次元観察子を理解する」点においては行き着く所は一緒で、表現方法と説明方法が変わったと理解すると良い。
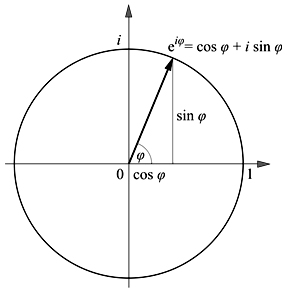
この複素空間モデルは、数学の界隈でも有名な「オイラーの公式」を使用している所がポイントである。
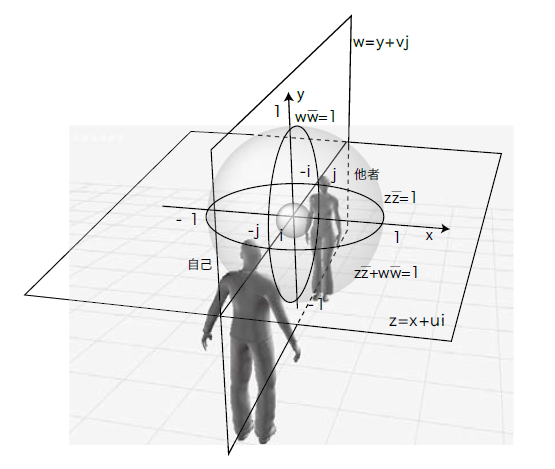
以前に『エーテル空間を知覚していく』の項で、書籍『シュタイナー思想とヌーソロジー』を引用して以下の図を出したが、これも複素空間モデルの話である。
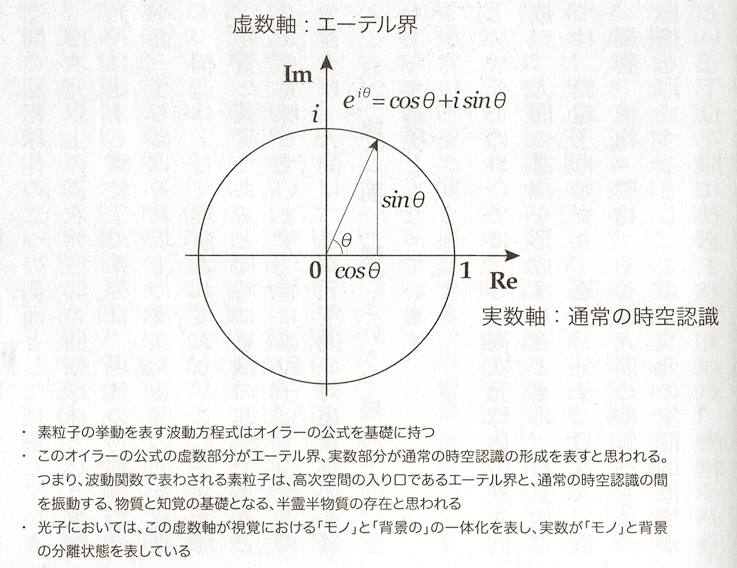
この図においてはx軸方向の値が実数、y軸方向の値が虚数となっている。
二つの軸を言い換えると実数軸と虚数軸となる。
このように実数と虚数の座標で表現できる空間を、数学では「複素二次元空間」と呼ぶ。
こうした数学的なものを意識の構造として説明する所がヌーソロジーの肝である。
複素空間モデルをじっくりと理解しよう
「複素空間モデル」について、これまでの次元観察子ψ3の説明を踏まえつつちゃんと理解しよう。
まず、「前」の発見が第一である。これは従来通りである。
以下の『4次元を発見するための図』を知覚正面に見立てて、垂直方向となる「前」を発見しよう。
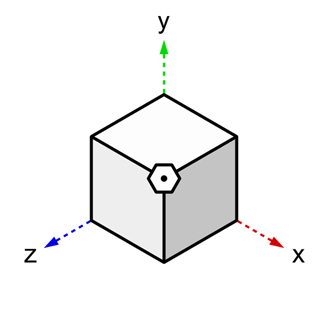
目の前の空間を「知覚正面」として見ることができた場合・・・
『人間の外面』や『主体』も分かってくる。
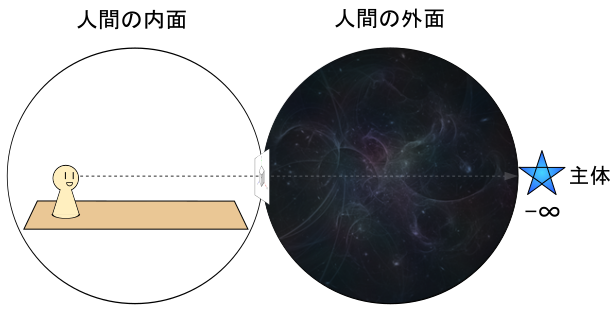
さらに、「奥行きを虚軸」とする。
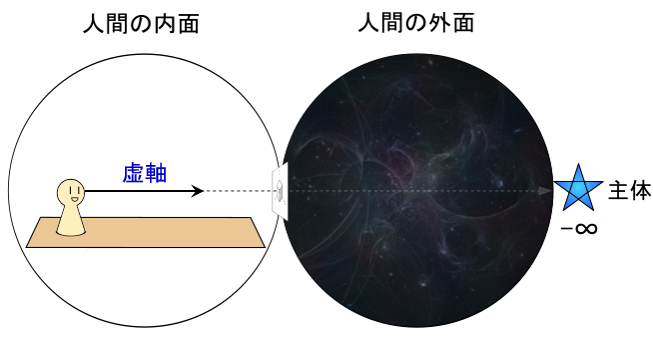
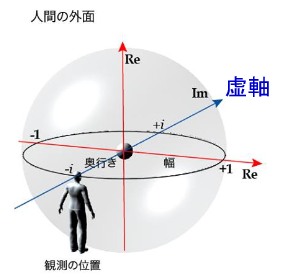
すると何が言えるのか?
虚軸を見ている人が「知覚正面」として目の前を見た場合、虚軸方向には距離が存在しないように見えるが・・・
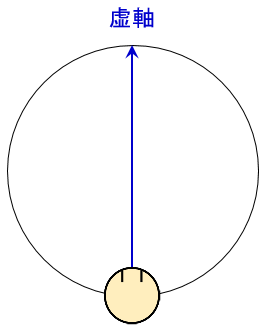
そこから90度回転した位置の真横からの視線だと距離が存在することが言えるのである。
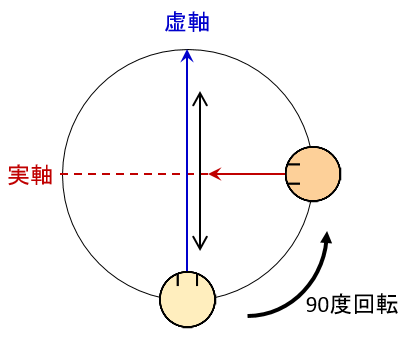
これで先ほどの図の意味も分かるだろうか?

つまり、旧来モデルでは「手前」や「後ろ」をψ4の位置とするが…
複素空間モデルでは「横からの視線」あるいは「幅」をψ4の位置とする。
さらに、複素空間モデルは「虚軸」を『奥行き』、「実軸」を『幅』と呼ぶ。
そうすると「自己にとっての奥行きが、他者にとっての幅であり、自己にとっての幅が、他者にとっての奥行きである」ということが言える。
前回の『キアスム』の説明で「自己にとっての見える世界が、他者にとっての見えない世界であり、自己にとっての見えない世界が、他者にとっての見える世界である」ということについて書いたが…
複素空間モデルにおいては「見える世界⇒奥行き」「見えない世界⇒幅」と置きかえると、同様のことが言えるわけである。
このように複素空間を解釈すると、以下の「オイラーの公式」の図が人間の意識の構造として使えるようになる。
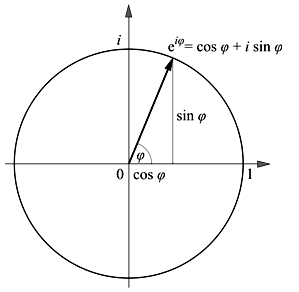
さらに、「オイラーの公式」は実際の量子力学の基礎で出てくるものでもあるため、量子力学で説明される素粒子の構造は、人間の意識の構造を説明するものにもなるわけである。
何故、半田さんは複素空間モデルを2013年から積極的に使うようになったのか?
やはり、初版の『人類が神を見る日』の帯にも書かれていた「素粒子の正体は、我々の意識だった!」の格言が重要だからである。

このことを理解していくためにも、複素空間モデルを併用して使っていこう。
ミクロに潜む複素空間モデル
複素空間モデルにおいて重要なことを一言でまとめると・・・
自己にとっての奥行きは、横側から見た他者にとっては幅である
ということになる。
つまり、先ほど説明した通り、以下の図のようになっているわけである。
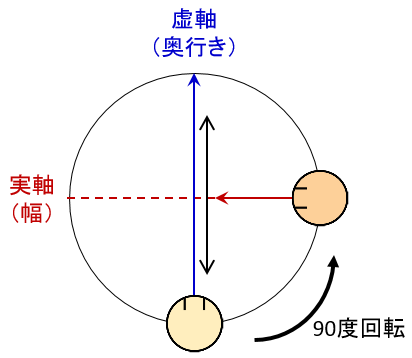
そして、これが分かったから何なのか?
ただこの仕組みを頭に入れただけでは意味がないかもしれない・・・
ヌーソロジーでは最終的に「奥行き」と「幅」も『等化』されるようになる。
つまり、「対称的で同一のように見なすことができる」ようになる。
ヌーソロジーの複素空間モデルの図は、それぐらい深い意味を持つものである。

果たして物理現象としてそんなことがあり得るのだろうか?
思い出して欲しいのは、この複素空間があるのは素粒子の世界であり、即ち「ミクロの世界」なことである。
原子や原子核の大きさは「約10のマイナス10乗m」や「約10のマイナス15乗m」といった数値になる。
したがって、複素空間モデルを意識するということは、それぐらい小さい世界を意識することと同義となる。
そのため、初めの方で説明した「ミクロを意識する」という基本に立ち戻る必要がある。

こうしたミクロの世界の中での思考に成功し、何かしらの体感を得なければ、ヌーソロジーが「分かった」とは言えないだろう。
以上。複素空間モデルについて分かっただろうか?
複素空間は「オイラーの公式」に含まれており、量子力学で実際に使う数式でもそれが出てくる。
![]()
しかしながら、こうした「難しそうな数式」が出てくると、一気にイメージがしずらくて悩む人もいると思うので・・・
次回はそれをイメージで理解する方法を探っていく。
↓続き
|
2013:The Day God Sees God 人類が神を見る日 [ digital edition ]
ヌーソロジーをちゃんと学習するならこれ! |




















やっとここまで、見ました。
一年前ヌースに出会ってからの、復習、
ヌース語の解釈、動画などなど、とても、ありがたかったです。
サロンのビギナーズには、超おすすめですねー。
以後、更新期待してまーす♪
>Mi.Fさん
感想ありがとうございます!
理解できるものを目指して書いてるので嬉しいです。