■変換人型ゲシュタルト論(60)　～ψ6側の「回転」と「無数化」～

不定期連載『変換人型ゲシュタルト論』シリーズ。　記事一覧はこちら。

---

前回に引き続き、『次元観察子Ψ6』の説明を詳しくやっていこうと思う。

・・・とはいえ、これは『次元観察子Ψ5』ほど抽象的な話にはならない。

例えば、我々が普通に他者の視線を意識したとしよう。
あるいは、他者のことを考えて、それらがどのように世界を見てるかをイメージするとしよう。

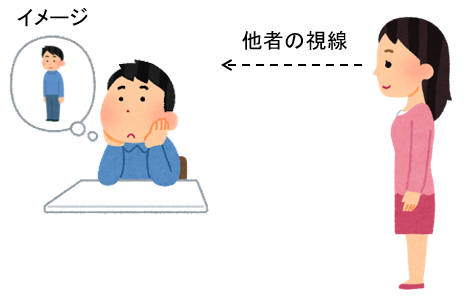
それによって、自身が他者のことを考えた行動をすることができたり、自身が他者のためになるアイデンティティを形成することができる。
そうした意識形成の先にΨ6がある感じである。

また、Ψ5を理解するための鍵となる概念は「回転」と「無数化」だった。そして、Ψ6を理解するための鍵となる概念も「回転」と「無数化」なのであるが・・・それはΨ5ほどイメージの難しいものではない。
ごく普通に回転をイメージしたり、ごく普通に無数化をイメージしたりすれば良い。

そんなわけで、Ψ6における「回転」と「無数化」について説明しよう。
　

回転

まず、とある物体があったとしよう。

その物体は一面だけではどうなっているか分からない。2D（2次元）である。
そのため、全貌がどうなっているかを把握するには回転させる必要がある。
そうすると、3D（3次元）としてそれを正確に認識することができる。

また、あらゆるものに対してこれを行うことで、3Dとして世界を認識することが定着する。
自身が動いて世界を見渡したり、物を手にとって操作したりすると、色んな物の色んな面を見ることができる。
これは「物を回転させて、その物を3Dとして認識する」ことと同義であり、世界を3Dとして認識することとも同義である。

以下の『視点変換3Dルーム』でも、部屋を動き回ることで、世界や物の色んな面をみることが分かるだろうか？
これは「回転」によって世界の全貌を3Dとして把握していることと同義である。

◆視点変換3Dルーム

このように、Ψ6の回転は、本当にただ物を回して、3Dとしてそのものを把握するだけである。

一方、Ψ5の場合は例えば以下の図を使って「４次元空間」を発見して、知覚正面を認知して、それを回すみたいなことをしていたが・・・

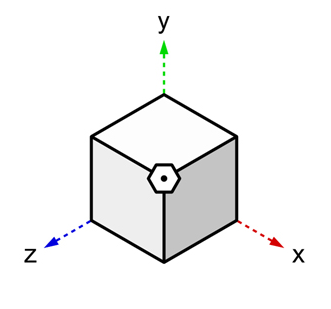
Ψ6の場合はそこまで考えなくて良い。
普通に物が回っていて、自身の視線とその物の間には、ちゃんと「距離」があることが分かっていれば良い。

簡単な話であるが、分かっただろうか？
　

無数化

次に、「無数化」についてである。
これもただ「数え切れないほど増やすだけ」のイメージで大体正しい。

まず、『次元観察子Ψ6』より一つ次元を落として・・・
『次元観察子Ψ4』の場合は、他者の視線を1本だけ意識するだけであった。

そして、『次元観察子Ψ6』の場合は、他者の視線をたくさんの数（無数の数）意識する。

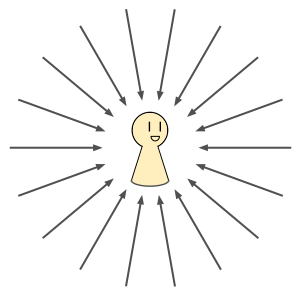
大体それがイメージできればOKである。

また、この時、視線の数だけでなく、時間軸においても「無数化」が行われていることが重要である。

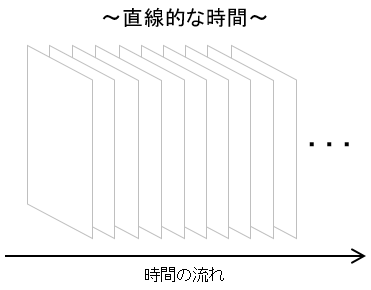
自身の肉体が動いている時、それは直線的な時間の中で動くアニメーションのように捉えることができるのが分かるだろうか？

アニメーションの中にある１枚１枚の絵はそれぞれ単一のイメージに過ぎないが、時間軸にそってそれを無数に増やすことで、無数のイメージから自身の肉体の動きを捉えることができるわけである。

また、自身が回転しているアニメーションによって、自身の身体の全貌を認識している時も、それと同様のことが起きている。

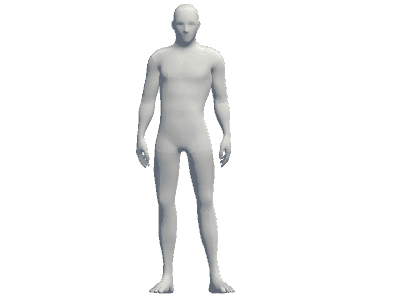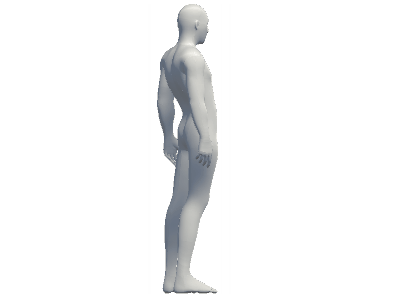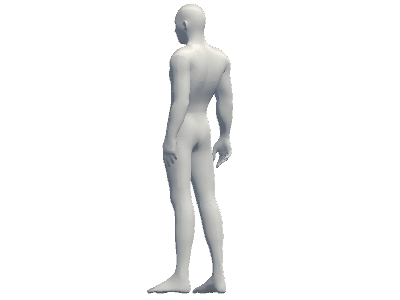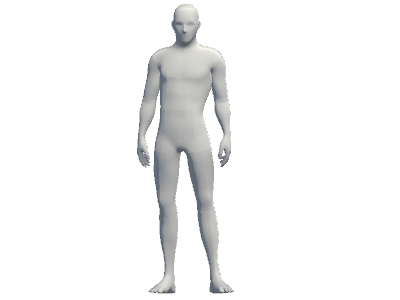
以上のように、通常の時空における「回転」と「無数化」が理解できれば、Ψ6における回転と無数化の理解は大体OKである。
　

主体の無数化に対する、客体の無数化

さらに、「無数化」ということで、『次元観察子Ψ6』の場合は「客体の無数化」が起きていると考えれば良い。

『次元観察子Ψ3』と『次元観察子Ψ4』では以下のように「主体」と「客体」があった。

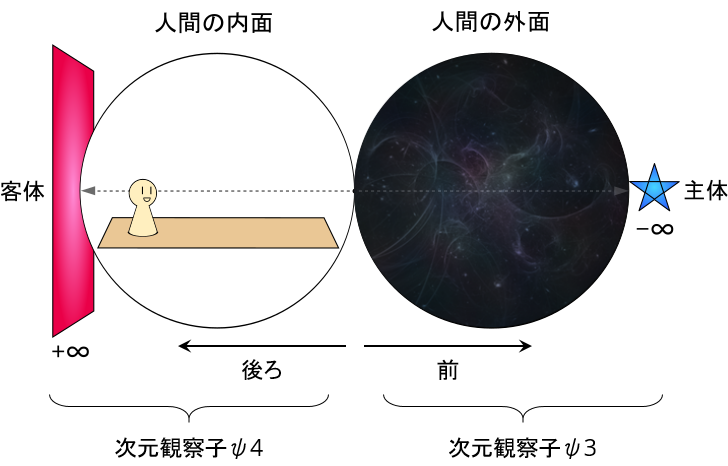
『次元観察子Ψ5』の場合は「見ること」を主とする「主体」が無数になるので、以下のようなイメージになるとした。

それと同様のイメージでいくと・・・『次元観察子Ψ6』は「見られること」を主とする「客体」が無数になるので、以下のようになる。

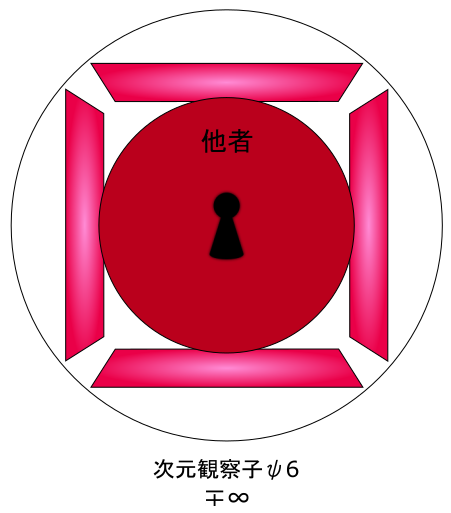
これはΨ5と比較するための簡易的なイメージだが・・・分かっただろうか？

以上で説明したように、Ψ6に関しては、物が回転するアニメーションのイメージや、無数の視線があるイメージが分かれば基本はOKである。

　
↓続く

■変換人型ゲシュタルト論(61)　～3Dゲーム内の身体～