不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
◆◇等化は「無数化」の方向にある◆◇
ここまでの説明で『次元観察子ψ3』についてが分かっただろうか?
分からないだろうか?
『次元観察子ψ1』と『次元観察子ψ2』の『等化』によって分かる『次元観察子ψ3』は、
『等化』を理解するためにも核心となる所である。
あらためて説明すると、『等化』は「対称性が分かる」という意味であり・・・
ψ3においては「ミクロとマクロの対称性が分かる」ということになる。
これを言い換えると「ミクロとマクロが入れ替え可能で同じようなものに見える」ということにもなる。

したがって、等化が起きた時には、実は「マクロがミクロのようになる」みたいな現象が起きるのである。
安易なイメージだと、マクロって概念に対してミクロって概念がどんどん浸食して上書きされるイメージ?
(マクロは偶数系なので赤。ミクロは奇数系なので青のイメージ)
それから、ミクロは「一点」で、マクロは「全体」とほぼ同じ意味である。

そこで、ミクロとマクロが等化するとどうなるのか?
「全体(マクロ)」に対して「一点(ミクロ)」が無数に敷き詰められたような状態になるとも、言うことができる。
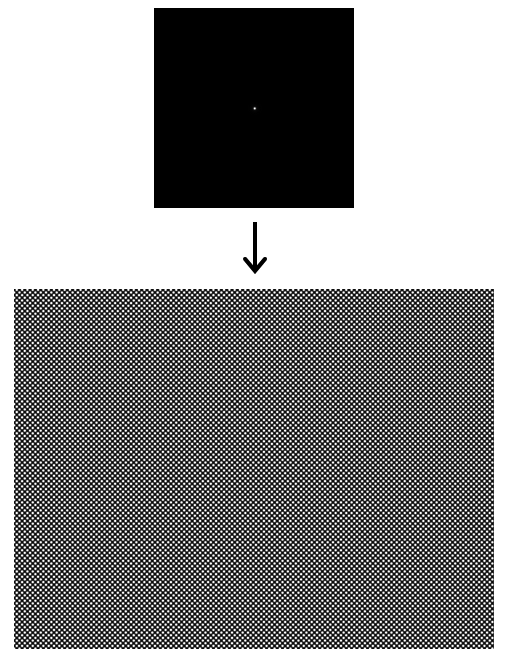
(上記の図は例えなので有限的な表現だが、もっと無限のミクロが空間全体にある感じ)
そして、実は『等化』は『負荷』側のものが無限のようにたくさんある状態になることと同義なのである。
今回の場合は「負荷⇒ミクロ」なため、ミクロがたくさんある状態である。
たくさんある状態になるということは「数かぎりなく多いことになる」という意味で「無数化」とも呼べる。
ミクロが「無数化」すると、マクロのような存在にもなり、「入れ替え可能で同じようなものに見える」こととも同義になってくる。
このように、等化は「無数化」の方向にあるという原理は、ψ1~ψ2の等化だけでなく、ψ3~ψ4の等化でも出てくる。
今後のヌーソロジー学習でもずっと出てくるため、頭に入れておこう。
光速度イメージと無数化
それから、どういう時に「ミクロの無数化によるマクロとの等化」の現象が起きるのか?
以前に「光速度のイメージ」についてを説明した。
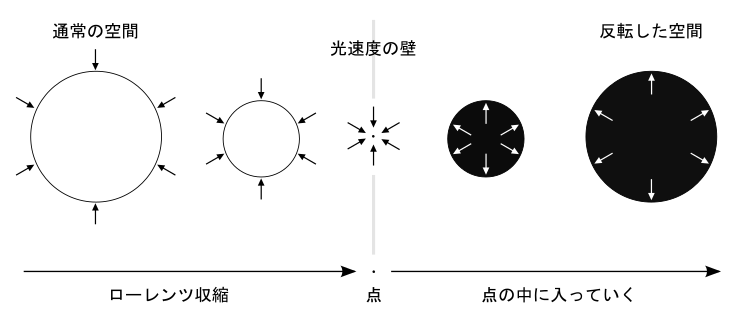
「光速度のイメージ」のように点の中に入ることができた時、そこから先に『人間の外面』があるわけだが、その臨界点は「光速度の壁」と一致して点になった時である。
その時の状態は、完全に「一点(ミクロ)=全体(マクロ)」になっている状態なので・・・
実は「全体(マクロ)に対して一点(ミクロ)が無数に敷き詰められたような状態」とほとんど一致しているのである。
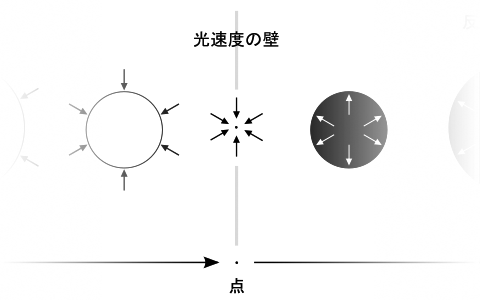
一=全?

全=一?
それらの関係が分かってくると、『人間の外面』についての理解がもっと深まってくると思う。
以上。「無数化」について説明した。
この「無数化」という発想は、次元観察子ψ3と次元観察子ψ4を等化する時にも出てくるので・・・
『変換人型ゲシュタルト論』でこれからも出てくるものとして覚えておこう。
↓続き
|
2013:The Day God Sees God 人類が神を見る日 [ digital edition ]
ヌーソロジーをちゃんと学習するならこれ! |