■変換人型ゲシュタルト論(34)　～次元観察子ψ4の話に入ろう～

不定期連載『変換人型ゲシュタルト論』シリーズ。　記事一覧はこちら。

---

◆◇次元観察子ψ4の話に入ろう◆◇

これまでは『次元観察子ψ3』の話をしてきた。
ここからはその次である『次元観察子ψ4』の話をしていこう。

奇数系である次元観察子ψ3については「反転した空間」にあるため抽象的な上に重要なので説明にとても長い手間をかけたが、
偶数系である次元観察子ψ4は「普通の空間」にあるもので、それよりも説明が容易なため、サックリと説明して進めたい。

以前にも説明したがψ3が「前」にあるものとした上で、
「後ろ」にあるものがψ4である。

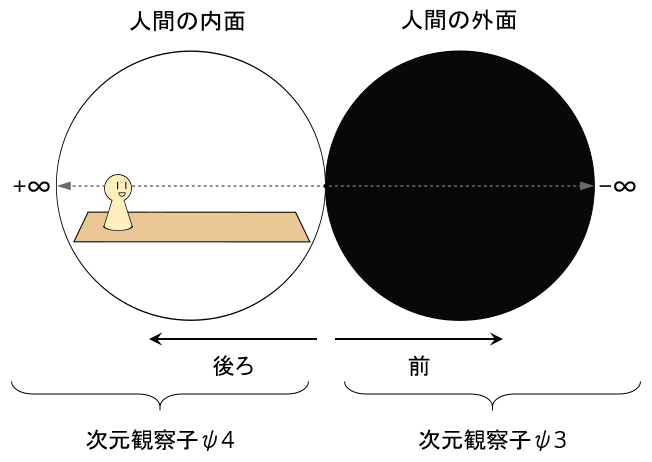
また、ψ3とψ4はどちらも「無限遠点」にあるとされている。
しかし、両者の意味は違う。
ψ3側の無限遠点は前方向にあり、「反転した空間」もとい「4次元空間」にあるとされていて、これは「－∞」と表記される。
ψ4側の無限遠点は後ろ方向にあり、これは「＋∞」と表記される。
この意味はψ3側の無限遠点よりも単純で、
「われわれが考えうる無限の遠さにある点」と同様の意味である。
つまり、とてつもなく遠いようなものである。

これは次元観察子ψ2の「マクロ」が表す「無限」とも近い。

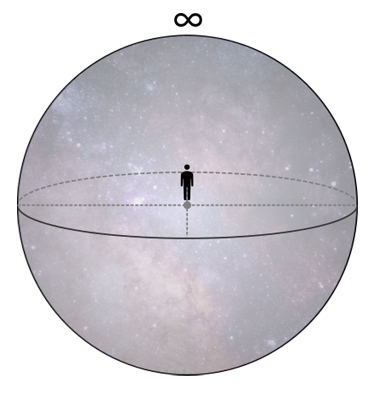
しかし、ψ4とψ2の違いは、『垂子』の線上を意識して
「ψ3の後ろ方向にあるもの」として捉えるかどうかである。

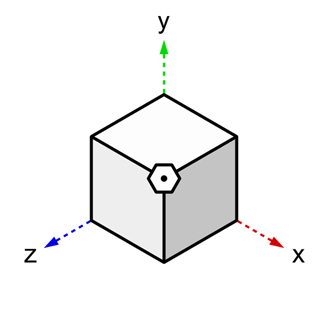
垂子は上記の「4次元を発見するための図」で立方体に垂直に差し込まれる線の方向にある。
そこで「4次元」が発見できた時の「後ろ方向の無限遠点」に『次元観察子ψ4』があると理解しよう。
　

主体と客体

また、ψ3の無限遠点に『主体』があるように、
ψ4の無限遠点には『客体』がある。

書籍『2013:人類が神を見る日』にも、
「ψ3が主体を構成している空間ならば、ψ4は客体を構成している空間ということになるのだ」と書かれている。

客体を以下のシンボルとして表してみよう。

すると、ψ3～ψ4については以下の図のようになる。

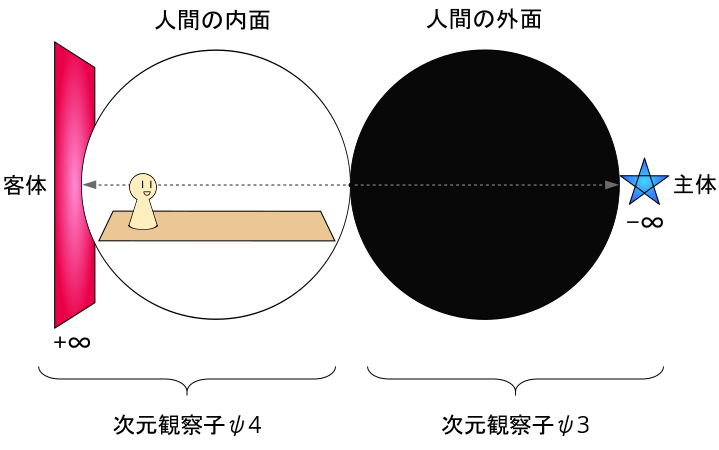
さらに、ψ3は「見る」意識であり、
ψ4は「見られる」意識であることが重要である

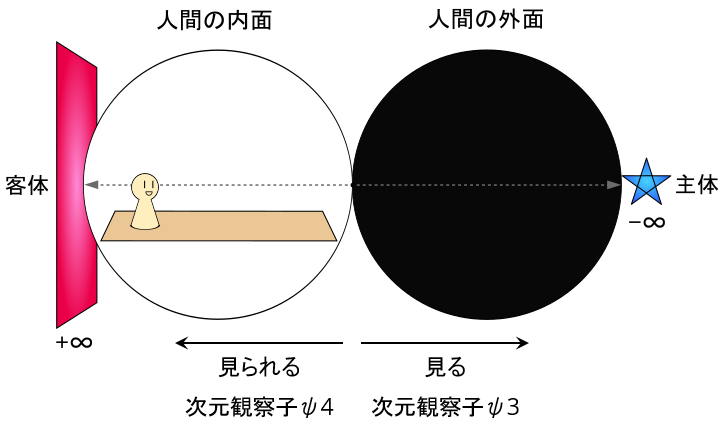
前側は「見る」、後ろ側は「見られる」の関係になっていることも、ヌーソロジーの基本となるので覚えておこう。

以上の基本を頭に入れれば、
次元観察子ψ4についてが分かってくると思う。

　
↓続き

■変換人型ゲシュタルト論(35)　～「鏡像段階論」について～