不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
引き続き、『次元観察子ψ5』を理解するための話をしていこう。
今回のタイトルは「『二重反転』をやってみる」である。
・・・ということで・・・
「反転」のイメージを工夫して『次元観察子ψ5』をイメージすることをやってみよう。
以前、『次元観察子ψ3』を理解する所で「光速度による反転」の話が出てきた。
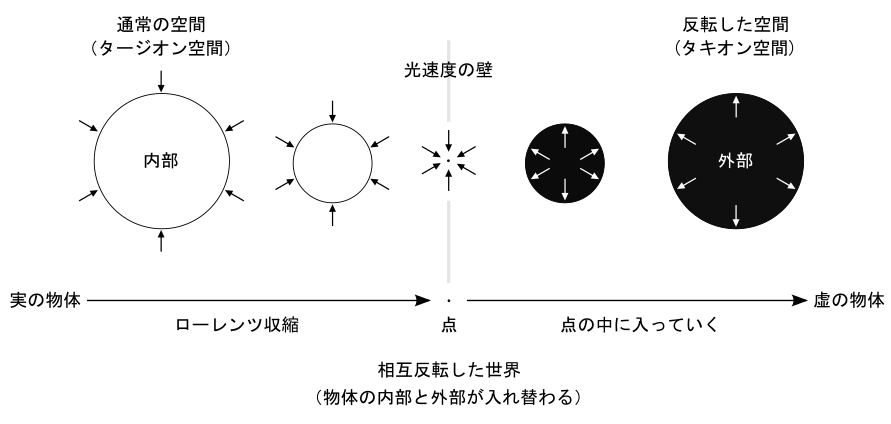
今回はこれを応用して「二重反転」みたいなことをやってみよう。
まず、以下のような構図が基本にあることを踏まえて・・・
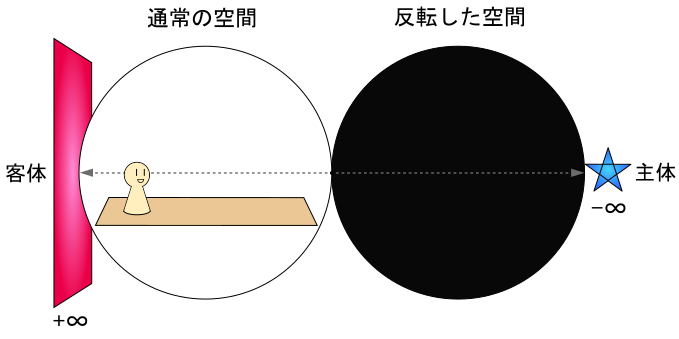
「通常の空間」と「反転した空間」と「主体」と「客体」と「自分自身」を以下のように配置してイメージしてみる。
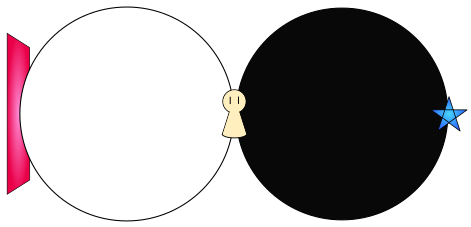
そして、それらがミクロの大きさに畳み込まれていくイメージをしていこう。
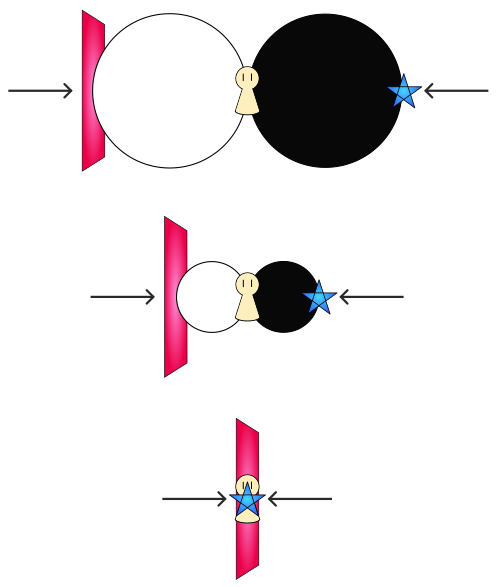
それが一致した位置に「自己」があるわけである。
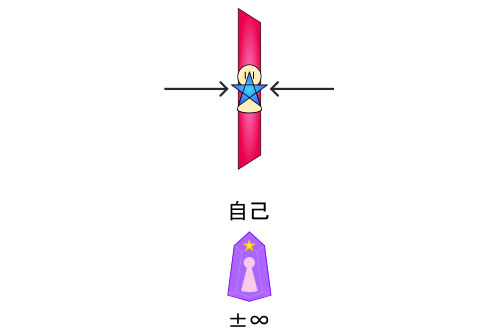
そして、このことは「通常の空間（ψ4）」と「反転した空間（ψ3）」の『等化』を意味していて、『次元観察子ψ5』のある位置にもなっている。
さらに、空間が光速度によって裏返るように・・・
「通常の空間」と「反転した空間」の双方がさらに同時に裏返って、つきぬけてくとどうなるだろうか？
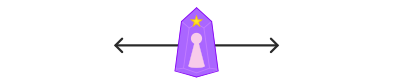
そうするとそこに「線」があるはずなので・・・それをあちこちの方向へ行くように回転させてみる。
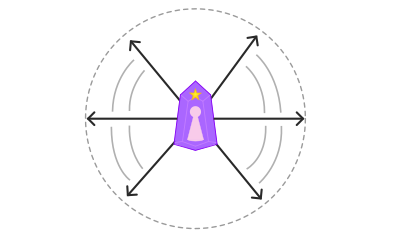
すると・・・「主体」が周りに無数ある世界が定着するのではないだろうか？
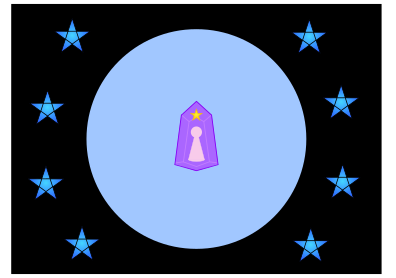
上記のようなイメージによってピンと来れば、『次元観察子ψ5』やヌーソロジーの理解がさらに深まると思う。
（続く）
