不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
◆◇基礎用語② 負荷・反映・等化・中和◆◇
引き続き、ヌーソロジー用語についてである。
ヌーソロジー学習の基礎となる、オコツトが言ったとても重要な4つのワードがある。
それは『負荷』『反映』『等化』『中和』の4つである。
この4つはそれぞれ数字の「1」「2」「3」「4」に対応している原理でもある。
まずはそれぞれについて軽く説明しよう。
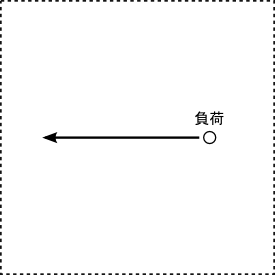
負荷
とある始原となる存在があったとして、
そこから開始する作用にあたる。
数字では「1」に対応する。
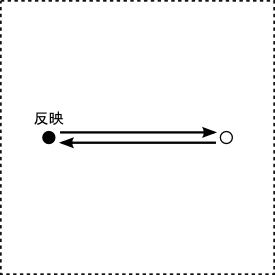
反映
『負荷』という開始の力に対して生まれる、
それとは逆向きの作用にあたる。
数字では「2」に対応する。
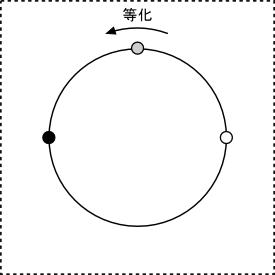
等化
『負荷』と『反映』という、
背反するものを統合するような「回転」の作用、
または、対象性を見出す作用にあたる。
数字では「3」に対応する。
『負荷』と『反映』を新たな次元の視点で見る力を持つ。
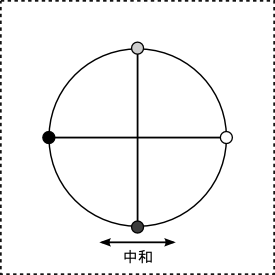
中和
『等化』の回転に対する逆回転。
回転が相殺されるため、その意味で、『中和』は「分離」するような作用にあたる。
また、双方の対象性を見出すのを拒む作用にもあたる。
数字では「4」に対応する。
新しい物質を誕生させるような力を持っている。
それから、「負荷と反映」や「等化と中和」の二つは対立関係にあり…
そのことを『対化』と呼ぶ。
例えば、負荷と反映の対化は、等化に向かうこともあるし、中和に向かうこともある関係である。
4つの原理と自他関係
上記の『負荷』『反映』『等化』『中和』の4つをもうちょっとイメージしやすいように説明しよう。
この4つの原理は数がある所にはどこにでも出てくるような概念である。
「自己×他者」関係でも出てくるし、次元幾何学でも出てくるので、それらをベースに説明してみよう。
負荷:始まる。ただ自分がいる
「ただ単に始まる」「一方向のもの」みたいな意味で良い。
次元的には点だけなので、零次元の状態である。
反映:受け手がいる。相手がいる
相手が出てくることによって多様な事象が起きる礎となる。
次元的には二点が停止してると一次元の線が出来て、
円運動すると二次元の場が生じる。
等化:俯瞰(ふかん)する者がいる。次元上昇
「次元上昇」を意味する特別な概念。
「負荷と反映を対称的に見ること」と説明がされている。
次元的には三点が停止してると二次元の面が出来て、
z軸方向への回転が起きると三次元の場が生じる。
中和:第三者の相手。安定する
「等化」に対する「反映」と同義。
3番目までだと不安定なため、新しい次元が安定する。
次元的には4つの点があると最低限の三次元立体(=正四面体)ができる。
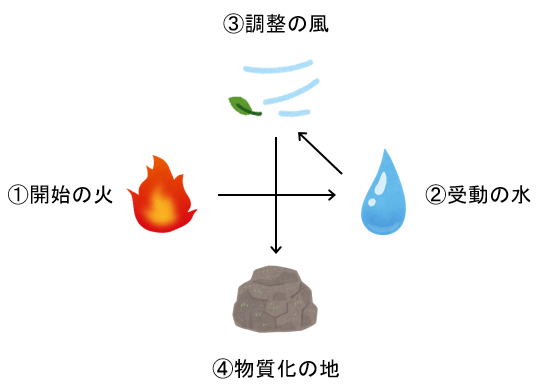
上記の4つは、疑似的なものだと以下みたいなイメージになってくる。
・負荷(始まる)
・反映(受ける)
・等化(俯瞰して捉える/調整する)
・中和(安定する/物ができる)
これらは万物にある究極元素みたいなものなので、
四大元素のイメージ(火・水・風・地)とちょっと絡めてみるのも良いかもしれない。
等化と中和について詳しく
上記の4つの『等化』と『中和』についてはなかなか理解が難しく・・・
特に『等化』はどちらかというと人間離れした概念みたいなものなので一層難しい。
詳しいことは以下でも書いたので、そちらも参考にしてもらいたい。
ペンターブシステムと次元観察子
さて、『負荷』『反映』『等化』『中和』の4つの原理に加えて、
さらに4番目の次の5番目は、次の1番目(新たなる負荷)になるという原理がある。
新たなる負荷
4番目より次に進むと、それがさらに新しい『負荷』になり…
[5⇒1(負荷),6⇒2(反映),7⇒3(等化),8⇒4(中和)]と進んでいくようになる
このように、5区切りで次に発展するシステムを『ペンターブシステム』と言う。
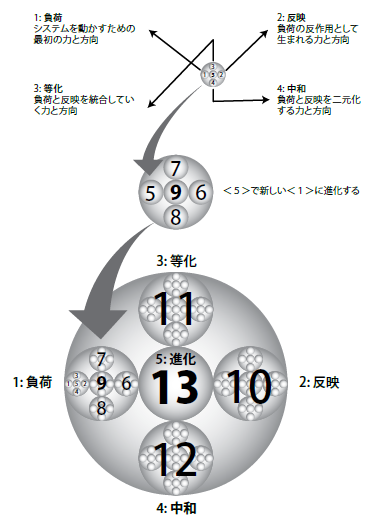
書籍『2013:人類が神を見る日』より引用
それから、なんでこのペンターブシステムの話が大事かというと…
前回説明した『次元観察子』がその構造を持っているからである。
[1,2,3,4]⇒[5,6,7,8]⇒[9,10,11,12]⇒[13]の発展構造は、そのまま『次元観察子ψ1~ψ13』にも当てはまる。
あと、13番目の反映となる14番目がある。
これは前回の「なんで次元観察子はψ14までとされてるのか?」に対する解答である。
書籍『2013:シリウス革命』の出版は1999年で、その時は12や13までとするのが主流だったが、2000年代に入ってからのヌーソロジーで、次元観察子は全部でψ14までとするのが主流となっていた。
恐らく、14番目はオコツトがよく分かっていない次元であるが、人間ならよく分かる次元である。
人間視点でヌーソロジーが分かってくるほど、14番目が大事になってくる。
「数は霊である」の文化
数字の「5」を区切りとするペンターブシステムについて、書籍『2013:シリウス革命』では以下のことが書かれている。
彼らは、まず「5」という数を無限の象徴として扱う。妙な言い方になるかもしれないが、 彼らは「1」よりも「5」が先行して存在していると考えるのだ。そして、この、数以前と も言える至高の「5」によって、「1」の観念を作り、これを存在が出現するための負荷と定義している。 次に、そうやって生まれてきた 「1」から、続く「2」「3」「4」「5」までの数に例のタカヒマラにおける基本概念 定質、性質、反性質、反定質などの意味合いをそのままダイレクトに当てはめ、宇宙のベーシックな構造を組み立てている。つまり、彼らにとって数とは言語そのものなのである。
数を「言語」とか「象徴」とか、時には「霊」のように生命を持ったものとして扱う文化は古代にもあった。
特に古代エジプトには確実にあった。

紀元前の古代エジプトで数学が発展していたことは、数学史や考古学でもよく知られているが・・・
それだけでなく、幾何学や数字には「霊」が宿るような、時には「神」との交信にまで使われるような、そんな神秘的な世界観を含んだ数学だったのである。
恐らく、王(ファラオ)信仰や太陽信仰の影で、秘教とか密儀とかの類の中でそれが伝えられていた。
古代エジプトの「数は霊である」というような文化がギリシャに伝わって「ピタゴラス数秘術」ができて・・・
ユダヤ人に伝わったものがユダヤ神秘主義の中で受け継がれ、それが後に「カバラ」となる。
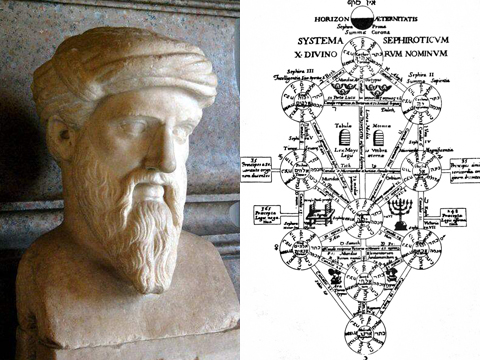
このように、「霊学」と「数学」が一体になったようなものが古代にあって、ヌーソロジーもそれに近いような印象がある。
ヌーソロジーは、量子力学誕生以降の20世紀末に復活した「霊学×数学」みたいなジャンルと言えるかもしれない。
↓続き
|
2013:The Day God Sees God 人類が神を見る日 [ digital edition ]
ヌーソロジーをちゃんと学習するならこれ! |