不定期連載『変換人型ゲシュタルト論』シリーズ。 記事一覧はこちら。
◆◇プログラム1 次元観察子ψ1~ψ2 方向の対化◆◇
いよいよ変換人型ゲシュタルトの本論の説明へと入っていこう。
まずは今現在われわれがいる位置とされる次元観察子ψ1とψ2の理解からである。

早速、書籍『2013:人類が神を見る日』より、以下の引用を参照する。
次元観察子ψ1とψ2は、現在あなたがたが空間と時間と呼んでいるものに相当しています
――シリウスファイル: 19900107(168頁)
人間の空間認識において、無限小から無限大へと向かうところに観察されている空間が次元観察子ψ1で、無限大から無限小へと向かうところに観察されている空間が次元観察子ψ2です。
――シリウスファイル: 19910512(177頁)
冥王星のオコツトによると、次元観察子ψ1は空間、次元観察子ψ2は時間と呼んでいるものに相当するとのことである。
それから、次元観察子ψ1は「無限小から無限大」、次元観察子ψ2は「無限大から無限小」へ向かうところに観察されるということで、
次元観察子ψ1はミクロ、次元観察子ψ2はマクロに対応するとも言われている。
つまり、以下のワードが次元観察子ψ1~ψ2の理解のための鍵となる。
次元観察子ψ1:空間・無限小から無限大へ・ミクロ
次元観察子ψ2:時間・無限大から無限小へ・マクロ
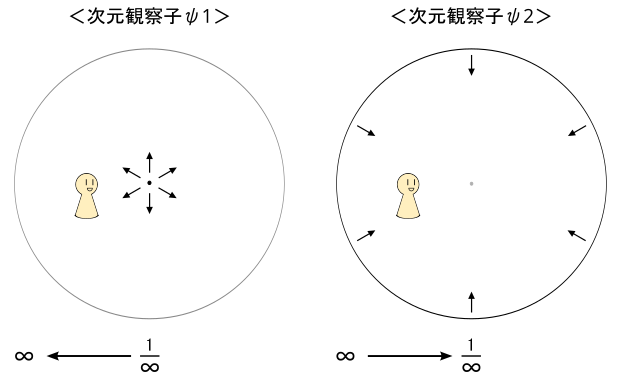
まずは、基本として空間と時間の対化、ミクロとマクロの対化が次元観察子ψ1と次元観察子ψ2であることを覚えておこう。
アニメーションにしてみる
オコツトの言う「無限小から無限大へと向かうところに観察されている空間が次元観察子ψ1で、無限大から無限小へと向かうところに観察されている空間が次元観察子ψ2」のイメージをアニメーションにしてみると、
以下のような感じになる。
次元観察子ψ1のイメージ

次元観察子ψ2のイメージ

次元観察子ψ1であるミクロと空間の関係は、ミクロから空間が広がる感じであり…
その反映が次元観察子ψ2のため、その逆が時間ということになるらしい。
こうしたψ1~ψ2の二つの概念に挟まれている次元を、ヌーソロジーでは『点球次元』と呼ぶ。
これがヌーソロジー的な「普通の世界」の基本となることを理解しておこう。
「表相」について
次元観察子ψ1~ψ2に関する話をもう少ししていこう。
それは『表相』という概念で説明されるものでもあるらしい。
これについては、書籍『2013:人類が神を見る日』を引用すると以下のように書かれている。
ただし、ψ1〜ψ2はもう一つ別の意味として解釈されることもある。それが本文の方にも何度か登場していた「表相」という概念である。表相とは、単純に言えば、ある角度から見た、対象の「見え姿」そのもののことをいう。
表相とは「ある角度から見た、対象の見え姿そのもののことをいう」であり、それもψ1〜ψ2の世界にあるものと解釈されるらしい。
これについては、以前に紹介した「視点変換3Dルーム」に出てくる
Kitcat実験の図で説明すると分かりやすい。


「ある角度から自身が見ている、KitCat缶の姿」もまた、ヌーソロジー的な『表相』と言えるわけである。
それから、「視点変換3Dルーム」で早速出てくる景色などもそうである。

我々にもこういった「世界を観測した景色」があって、その景色は見ている人によって違う。
わりと当たり前な話だが、ヌーソロジーの着実な理解はこうした常識からスタートする。
↓続き
|
2013:The Day God Sees God 人類が神を見る日 [ digital edition ]
ヌーソロジーをちゃんと学習するならこれ! |